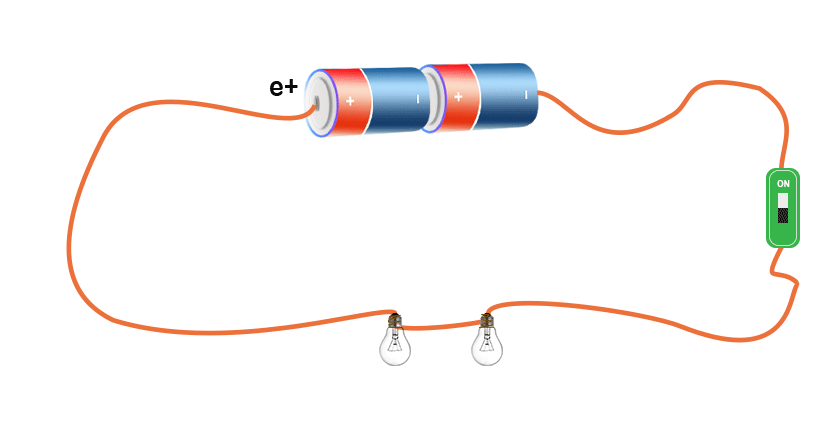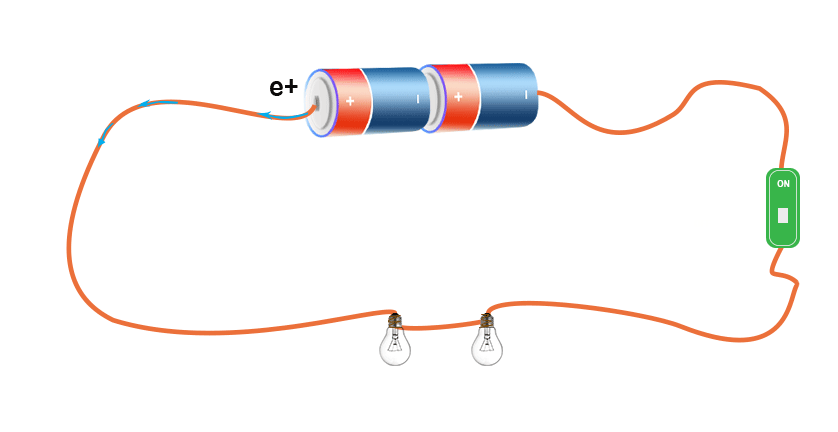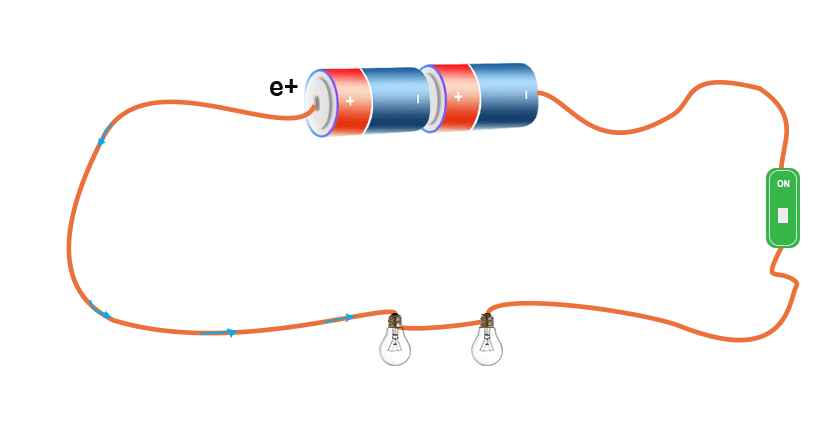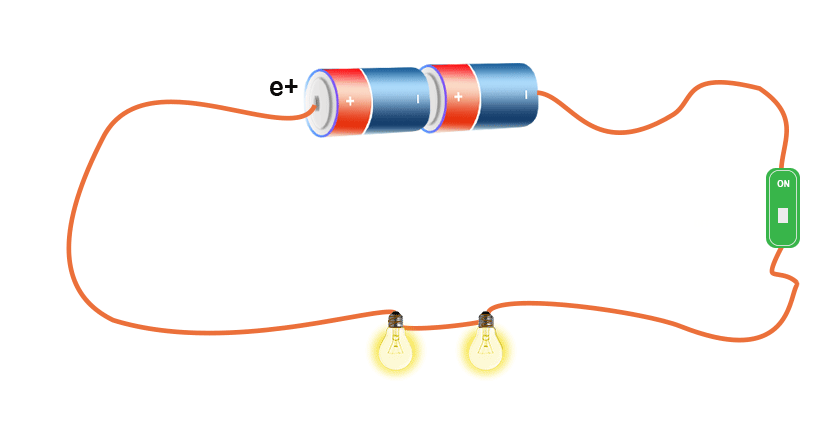
Current electricity is the flow of electric charges along a conductor. To maintain a steady flow of electric charges, two things are required. First, there must be a source of electric charges that is capable of moving and a way of causing it to move. Secondly, there must be a closed conducting path in which the charges move ultimately returning to the source. This closed path is called an electric circuit (see Figure 2.1). Copper wires are normally used as conducting pathways for the electric charges to flow. If focus is put on one point in the electric circuit for the purpose of determining the amount of electric charges passing that point in a given period of time, then the electric current has been determined.



The amount of the electric current in a material depends on the number of charges taking part and the speed at which they are moving. In a simple electric circuit, the charges that flow are the electrons.

Electric current is the amount of charge passing a given point in a circuit in one second. It is a fundamental quantity.

Mathematically,

Electric current, I = Quantity of charge, Q / Time, t

I = Q / t

But, Q = ne

Where: n = number of charges

e = charge of single electron

Therefore, I = ne / t

Thus, from the formula:
Electric current = Rate of flow of charge
= (the number of charge carriers per second) x (charge of a single electron)
From this definition, the SI unit of an electric current is coulomb per second (C/s) where, 1 C/s = 1 ampere (A).
Other units are milliamperes (mA), kiloamperes (kA) and microamperes, (µA). Their equivalence to the ampere are as follows:
1 A = 10³ mA
1 A = 106 μA
1 KA = 1 000 A.
When a steady electric current of 1 A is flowing in a circuit, a coulomb of charge passes a given point in the circuit per second. Coulomb is the SI unit of the number of charges flowing in a circuit.

A coulomb is the quantity of electricity which passes a given point in a circuit in one second when a steady current of one ampere is flowing.

Charge movement in an electric circuit

During the 18th century, Benjamin Franklin, American scientist and statesman, extensively studied both static and current electricity. He believed that in an electric circuit, it was the positive charges (the protons) that were moving, and his belief still defines the conventional direction of the electric current by the direction in which protons are thought to move.
In most electric circuits the electric current flows through conductors in which only negative charges (the electrons) can move freely. This implies that in most circuits, electric current is made up of moving electrons. Just as in a bicycle (see Figure 2.2), the chain allows energy to be transferred from the rider to the rear wheel; the chain does not carry energy. It is the motion of the chain that allows energy to be transferred. Likewise, the motion of the charges carried through a circuit transfers energy from one point to another. This means that the actual direction of an electric current is opposite to the conventional direction of electron flow.



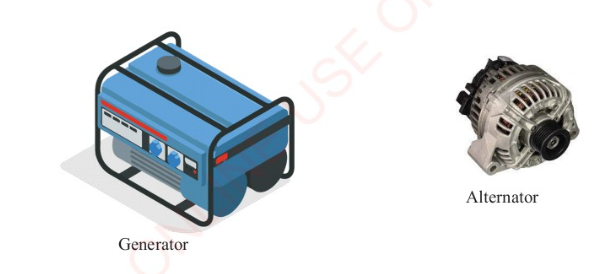
Sources of electricity
All sources of electric current work by converting some form of energy into electrical energy. The two basic sources are batteries and generators. Batteries convert chemical energy into electrical energy while generators and alternators convert mechanical energy into electrical energy. Figure 2.3 shows some sources of electric current.





Other sources of electric energy include water (hydroelectric power, water currents, ocean waves), sun, geothermal and wind. These sources are discussed in detail in chapter nine of this book.

Task 2.1
What are the 10 sources of electricity? How reliable are they? How do they produce electricity for use? Discuss.

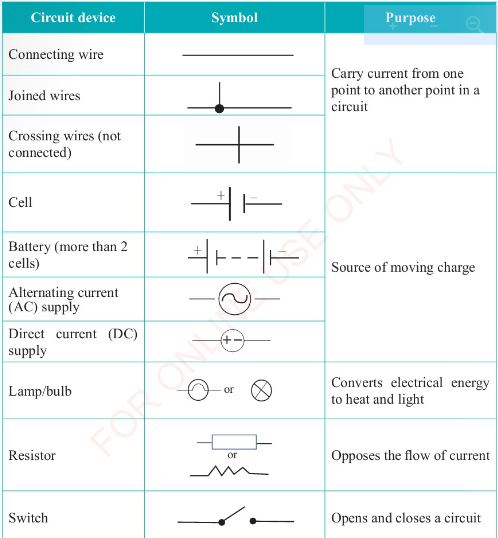
An electric circuit contains a source of moving charge (battery or generator), connecting wires made of a conducting material (usually copper metal) and various electrical devices such as bulbs, switches and resistors. The circuit may also contain devices for controlling the amount of current; these include rheostat, fuses and circuit-breakers, as well as devices such as ammeters for measuring current and voltmeters for measuring potential difference. Table 2.1 shows the list of some common circuit components, their purpose and the symbols used to represent them.
Table 2.1: Electric circuit components




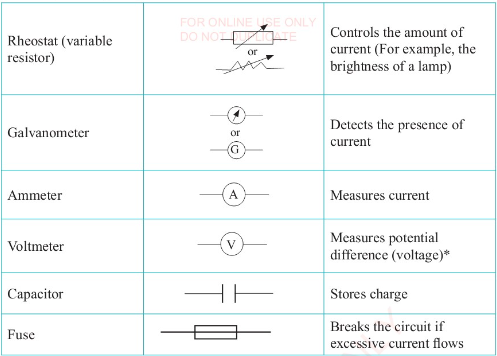
* Potential difference or voltage is the difference in the amount of electrical energy that charge carriers have between two points in a circuit.
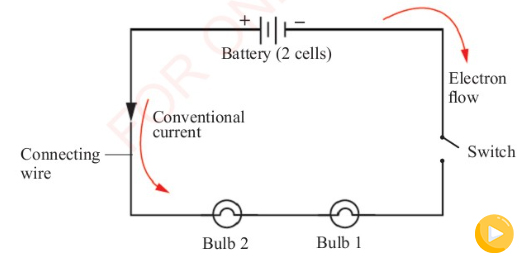
The potential difference between the positive and the negative terminals of a battery causes a current to flow along any conducting path that links them. Figure 2.4 shows two bulbs connected to a battery of two cells using copper wires. This combination of the battery, bulbs, switch and the conducting path formed by the copper wires make up a simple circuit.



Task 2.2
In groups, list the circuit components that you know. Draw a chart and indicate the use of each component and the electric symbol used to represent it. The best chart will be hung in the Physics laboratory.

In an electrical circuit, there is a close relationship between current, voltage and resistance.

An electric current is the rate of flow of charge through the material. In metals such as aluminium, gold, silver and copper, the charge is carried by free electrons. In solutions, such as sodium chloride, charge is carried by charged particles known as ions. Insulators like wood, plastic and rubber do not have free electrons since every electron is firmly bound in their atoms or molecules.

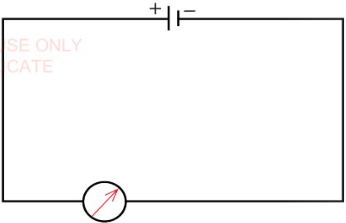
Detection and measurement of electric current
Since the electric current cannot be seen, it can however be detected by observing some of its visible effects. Such effects include the deflection of a galvanometer when connected to a circuit as shown in Figure 2.5. Galvanometers can detect very small currents of a few hundred microamperes.



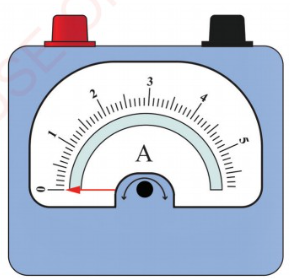
The rate of flow of electrons in a material is called electric current, and it is measured in amperes (A) using an ammeter shown in Figure 2.6. An ammeter is a calibrated galvanometer constructed with a known low resistance connected in parallel with galvanometer circuit. The pointer on the ammeter indicates the amount of current passing through it.



The ammeter is connected to a circuit in such a way that all the current flows through it. It is designed in such a way that its presence has little effect on the current. In essence, the ammeter acts like another connecting wire.
Ammeters are sensitive to the direction of the current implying that a wrong connection can damage them. Therefore, when connecting to a circuit, the red terminal (+) should be connected to the side of the circuit which leads to the positive terminal of the battery. The black terminal (-) should be connected to the side of the circuit which leads to the negative terminal of the battery.
With reference to Figure 2.4, the current in a simple circuit is the same at all points, or else the electrons could accumulate somewhere within the circuit or even leak away. The electrons leave the negative terminal of the battery towards the positive terminal via the connecting wires as in Figure 2.4. These electrons do so at the same rate as they flow into the positive terminal.
Note that, it is not necessary to change the direction of conventional current since the flow of electrons is effectively equivalent to a transfer of positive charge from the positive terminal to the negative terminal of the battery. In other words, the flow of negative charge to the right is algebraically equivalent to the flow of positive charge to the left.
Once the circuit is complete, electric charges inside cells start to flow out into the circuit. The cells provide the driving energy for the electrons. The electrons in turn lose all potential energy as they flow round to the other terminal. Energy lost to the bulbs is normally given out as light and heat.
The amount of electric current required to run various electric appliances varies depending on the intended use. For example, a car headlamp requires a current of about 4 A passing through it while a small torch uses about 0.2 A.

Activity 2.1
Aim: To measure current in a simple circuit.

Materials: Connecting wires, ammeter, battery, bulb and a switch.

Procedure
1. Using a battery, a bulb, a switch and connecting wires, construct a circuit that allows you to turn the bulb and off as shown in Figure 2.7.



2. Connect an ammeter in the circuit as shown in Figure 2.8



3. With the switch open, measure and record the current in amperes.
4. Close the switch, then measure and record the current as shown in Figure 2.9.



Do Activity 2.1

Question
Explain your observations and measurements.

In measuring electric current in the circuit, the ammeter must be connected in series with the battery and the bulb.
This arrangement enables the ammeter to experience the same amount of current in the circuit as the bulb. When the switch is opened, no current flows, light goes off and no reading is observed on the ammeter. When the switch is closed, current flows, light goes on and the ammeter reading is observed.

Example 2.1
An electric current of 0.12 A passes a certain point along a conducting wire. How much electric charge is flowing past this point in a minute?
Solution
Current = 0.12 A
Time = 1 min = 60 s
Required: Electric charge
Charge = current x time
Q = I x t
0.12 A x 60 s
= 7.2 C
Therefore, the electric charge flowing past the point is 7.2 C

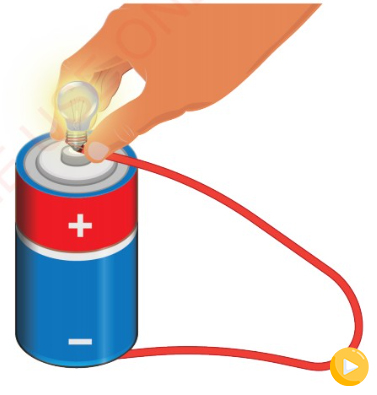
Every cell has a voltage, commonly referred to as potential difference across its terminals. It is this potential difference (p.d) that causes the flow of electrons (charges) in a circuit. For example, a dry cell shown in Figure 2.10 has a voltage of 1.5 V. This voltage is normally marked on the cell.



The larger the voltage, the higher the flow of electric current through a conducting medium and vice versa. Thus, voltage is defined as the difference in electric potential between two points. Voltage is measured using a voltmeter, as shown in Figure 2.11 (a). The SI unit for voltage is the volt (V).

A volt is the energy given to each coulomb of charge.





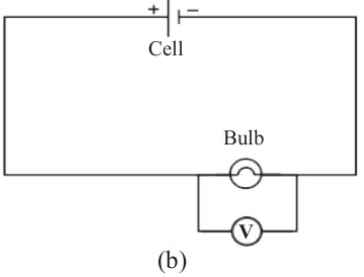
Voltmeter is connected across a component in a circuit, so that its positive terminal is connected towards the positive terminal of the battery and its negative terminal is connected towards the negative terminal of the battery. For such connection, a voltmeter draws very little current from the battery, and its overall effect on the current in the main circuit is almost negligible.
The potential difference (p.d) between the ends of a connecting wire is zero volts since there is almost no loss of potential energy over the section. Note that if 1 joule of potential energy is changed into other forms of energy when I coulomb of charge passes between the points in a circuit, then the p.d between the two points is 1 volt.
Sum of p.d around a conducting path = p.d across the battery terminals.

As current flows through the circuit, it encounters some opposition. This opposition determines the amount of current flowing in an electric device. All materials offer some resistance to the flow of electric current. Insulators offer high resistance while conductors offer low resistance. Amount of current flow depends on the voltage (p.d) across a material and the nature of the material.
The higher the resistance the lower the current for a given voltage.

George Ohm observed that voltage across a conductor was directly proportional to the electric current flowing through it provided that temperature and other physical conditions of the conductor were kept constant.

Hence, V oc I
V = IR
where R is the constant of proportionality.
This constant is called resistance and the above relationship is known as Ohm's law.

Ohm's law states that at constant temperature and other physical factors, a current passing through a wire (conductor) is proportional to the potential difference across its ends.
This implies that,
Resistance, R = p.d across the conductor, V / current through the conductor, I
Therefore, a resistance of 1 ohm is obtained when a p.d of 1 V causes a current of 1 A to flow in a circuit.
Resistance is measured in ohms (Ω). Other multiples of the unit are kiloohm (kΩ) = 10³ Ω, megaohm (ΜΩ) = 10 Ω, milliohm (mΩ) = 10 3 Ω and microohm (μΩ) = 10 6 Ω.

Resistors are the most commonly used electronic components that play a vital role in a circuit. These components are designed to offer specific resistance to the flow of an electric current in a circuit. They can maintain currents and potential differences at the levels needed for other circuit components to function properly.
A resistor whose value does not change with the change in voltage is called fixed resistor or standard resistor. Standard resistor values can be checked from a resistor colour-code chart. Resistors whose values can be changed by the experimenter are called variable resistors. The rheostat in Figure 2.12 (a) is an example of the variable resistor. Figure 2.12 (b) shows a fixed resistor with colour codes.

Sliding Contact

Terminal C

Terminal B

Coil of wire

Terminal A

Materials through which current flow is directly proportional to the p.d across them, at a steady temperature, are said to obey Ohm's law. They are referred to as Ohmic conductors.
A graph of voltage against current for an ohmic conductor is shown in Figure 2.13.



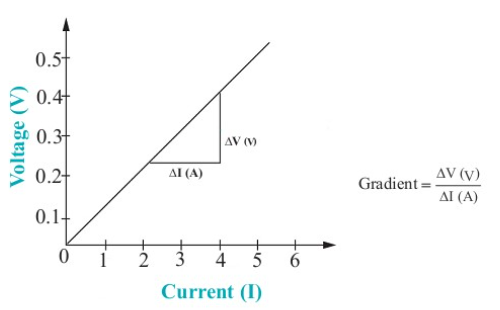
The gradient of the graph represents resistance. The gradient is constant. The resistance of a particular wire or conductor is constant. If the voltage is doubled, so will the current. The graph of voltage against current passes through the origin. The results obtained from various experiments have shown that the resistance of a conductor is affected by several factors. These include;

1. Length of the conductor
A short length of a wire has small resistance while a long wire of the same material and thickness has a large resistance.

2. Temperature
The higher the temperature of the conductor the higher the resistance and vice versa. The resistance of most metal conductors increases with increase in temperature, though this is much less in some cases than in others. In such a case the conductor does not obey Ohm's law. Hence:
(a) Constantan (copper - nickel alloy) is used in standard resistors since its resistance changes to a very small extent in a wide range of temperature.
(b) Connecting wires used in circuits have a very low resistance to keep the energy that is wasted elements of electric kettles and as heat to a minimum. Heating cooker are made from wires of known large resistance to ensure that heat (thermal energy) is released at a specific rate.

3. Nature of material
The conducting ability of a material has to be considered. A nichrome wire has higher resistance than a copper wire of the same dimension. This is why nichrome wires are used in heating elements of electric heaters. Also, due to its low resistance, copper is mostly used for connecting wires in circuits, including wiring in houses.

4. Cross-sectional area
A thin wire has higher resistance than a thick wire of the same length and material. The filament of a bulb is made up of a very thin tungsten wire. It therefore has a high resistance necessary to produce large amount of heat to light the bulb. Comparing copper and nichrome wires, these factors can be summarised as shown in Figure 2.14.



With all other factors being kept constant, a long wire has a higher resistance than a short wire, and a thin wire has a higher resistance than a thick one.

Construction of simple electric circuits
Figure 2.15 shows a circuit consisting of a battery, a switch and 2 bulbs.



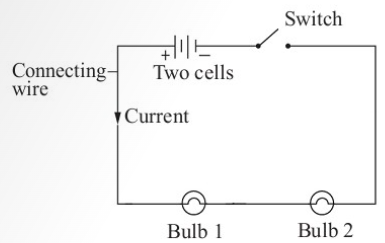
When the switch is closed, the current flows through the circuit, and the bulbs light up. The circuit is said to be complete. When the switch is opened, no current flows through the wire as the path carrying the current is broken. The circuit is said to be incomplete.
When constructing an electric circuit, we must be certain that there is a complete path for the current to flow from the battery through any external devices and back to the battery. It is a good idea to first sketch a schematic diagram of the circuit. On the diagram, use a pencil to trace the path the current will follow. You should be able to do this without lifting the pencil. Also, remember that the conventional current is the flow of positive charge, Physics for Secondary Schools so the current leaves the positive terminal of the battery and returns to the negative terminal.
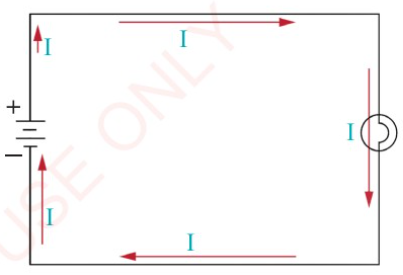
Consider a simple circuit containing two dry cells, a lamp and connecting wires as shown in Figure 2.16 (a). Figure 2.16 (b) is the schematic diagram showing the direction of the conventional current of this circuit.





A switch can be added to the circuit so that the light can be turned on and off as shown in Figure 2.16 (c).



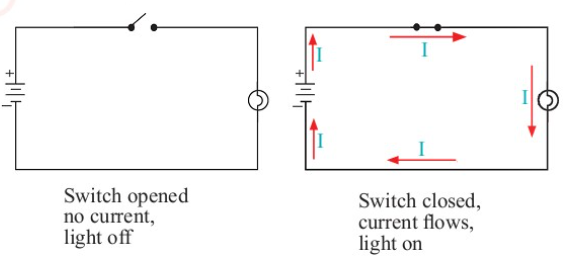
In order to control the brightness of the lamp, a rheostat has to be included in the circuit as shown in Figure 2.16 (d).



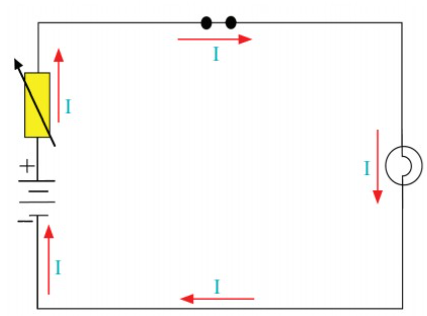
To determine the amount of current flowing in the circuit, an ammeter is inserted as shown in Figure 2.16 (e).



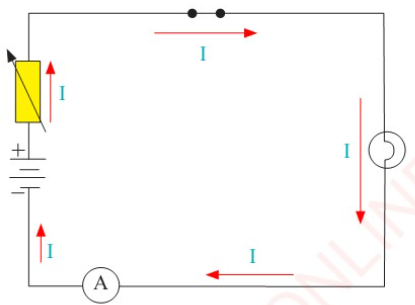
In a circuit, an ammeter is always connected in series to the battery. The current has to pass through the ammeter if it is to be measured. Unlike the ammeter, a voltmeter is connected in parallel to a component so as to measure the voltage drop across it. Figure 2.17 shows a simple electric circuit in which the ammeter and voltmeter are connected in series and parallel to a bulb, respectively.



As already learnt, resistance is the ratio of the potential difference across the ends of a conductor to the current flowing through the conductor. Radio and television sets contain large number of resistors, ranging from few ohms to millions of ohms. Some are made by winding wire while others are made from carbon or graphite. For connection purposes, resistors are provided with wire ends or terminals as shown in Figure 2.18.



Activity 2.2
Aim: To verify Ohm's law.

Materials: Voltmeter, ammeter, connecting wires, cell, variable resistor, unknown resistor, switch

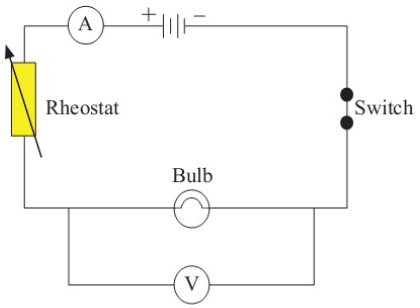
Procedure
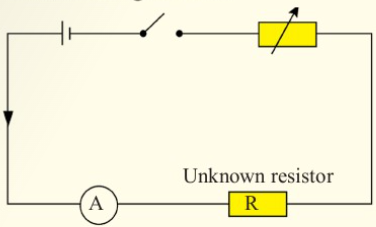
1. Connect a switch, an ammeter, unknown resistor and the variable resistor to the battery in series as shown in Figure 2.19.



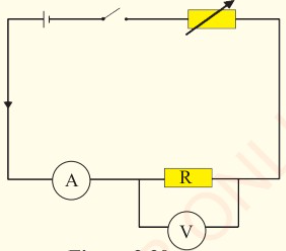
2. Connect a voltmeter parallel to the unknown resistor as shown in Figure 2.20.



3. Close the switch, then record the ammeter and voltmeter readings.

4. Adjust the rheostat so that the lowest possible current and corresponding voltage are obtained.

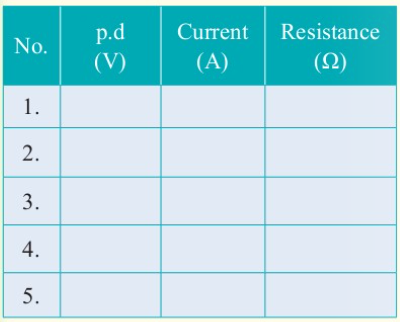
5. Move the sliding terminal of the rheostat to increase the current gradually. Record the values of current, I and potential difference, V in Table 2.2.



Do Activity 2.2

Question
Calculate the resistance of the unknown resistor.

The resistance of the unknown resistor, R is calculated using the formula: R = V / I The average of the values in the third column of Table 2.2 gives a value for the resistance of the unknown resistor. In the above activity, the rheostat (variable resistor) has been used for varying the current in a circuit. Note that, as the sliding terminal of rheostat moves, it varies the length of the conductor being used in making the rheostat.
Note: For a single loop or simple circuit:
1. Current is the same at all points around the circuit.

2. The sum of the potential differences around a conducting path from one battery terminal to the other terminal within the circuit is the same as the p.d across the battery.

Example 2.2
A resistance wire of 20 2 is connected across a battery of 5 V. Calculate the current in the circuit.
Solution
Resistance, R = 20 Ω
Potential difference, p.d = 5 V
Required: Current, I= ?
From; I= V / R
= 5V / 20 Ω
= 0.25 A
Therefore, the amount of current is 0.25 A.

Example 2.3
An ohmic conductor has a voltage drop of 9 V measured across it. The current flowing in the conductor is 3 mA. What is its resistance?
Solution
Voltage drop, V = 9V
Current, I = 3 mA =3 x10-³ A
Required: Resistance, R = ?
From; V=IR
R = V / I
= 9 V / 3 × 10-³ A
= 3000 Ω
Therefore, the resistance is 3 000 Ω.

Example 2.4
Calculate the readings of the voltmeter P and the ammeter Q in the electric circuit in Figure 2.21 when the switch is closed.



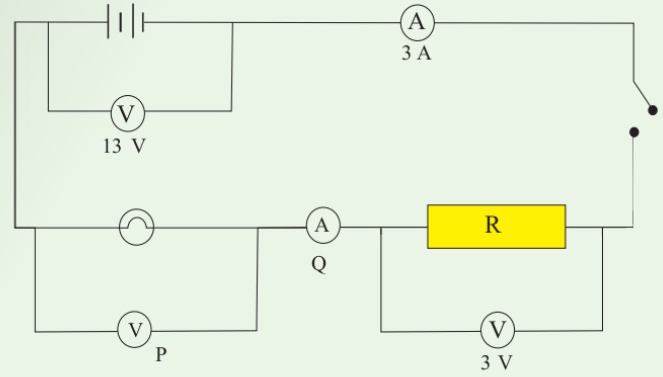
Solution
Being a single loop circuit, the current is the same at all points.
Therefore, the reading of ammeter Q is 3 A.
Sum of p.d in external circuit = p.d across battery
3V + P = 13 V
P = 10V
Therefore, the reading of Voltmeter P is 10 V.

Exercise 2.1
1. In an experiment to determine the value of resistance, the following results were obtained.



From the experimental results:
(a) draw a graph of Vagainst I
(b) determine the resistance R

2. A current of 0.25 A flows through a circuit of voltage 10 V across a bulb. What is the resistance of the bulb?

3. Describe factors that affect the resistance of a conductor.

4. (a) What do you understand by an ohmic conductor?
(b) A resistor has a resistance of 500 2. How could this resistance be measured experimentally?
(c) Which has a greater resistance; a long, thin, hot nichrome wire or a short, thick, cool copper wire?
(d) If a p.d of 6.0 V is measured across the ends of a wire of resistance 12 2,

(i) determine the current that flows through it.
(ii) calculate the p.d that is required to produce a current of 1.5 A flowing through it.

Task 2.3

In groups, collect wires of different thicknesses (cross- sectional areas) and carry out the following tasks inside the Physics laboratory.
1. Measure and record the lengths and thicknesses of the wires.

2. Use Figure 2.22 to construct a simple circuit that can compare the current passing through each of the wires connected between A and B.



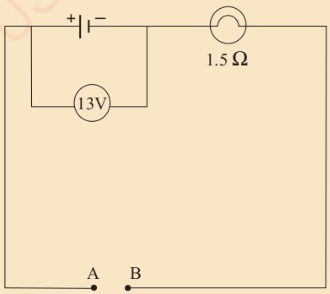
3. List the wires in their order of increasing resistance.

Connection of resistors
Resistors can be connected either in series or in parallel depending on the desired output.

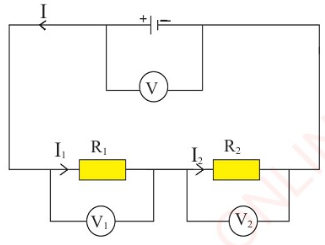
(a) Series connection
In series connection, the resistors are connected end to end as shown in Figure 2.23. In this case, voltages are additive. The total potential difference (V _T ) is given by;

V _T = V₁ + V₂

This means that the sum of the p.d across the resistors is the same as the p.d across the battery. The current is the same at all points around the circuit. That is;

I₁ = I₂ = I



From Ohms' law,
V = IR
Then,
V₁ = I₁R₁ and V₂ = 1₂R₂
V _T = I₁R₁+I₂R₂ = IR _T
Since the current flowing through the resistors is the same;
IR _T = IR₁ + IR₂

R _T = R₁ + R₂

Therefore, total resistance or equivalent resistance for resistors in series is equal to the sum of individual resistances.

(b) Parallel connection
Resistors are connected across two common points in a parallel arrangement as shown in Figure 2.24.



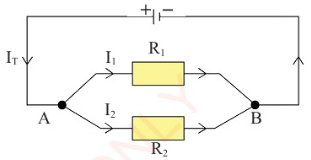
In parallel connection, potential difference is from a single source; so, it is the same for all the branches. However, the current is different in each branch. From Figure 2.24:
Total current I _T = 1₁ + 1₂
From Ohm's law;
V = IR
I = V / R
Then, I _T = I₁ + I₂
v / R _T = V / R₁ + V / R₂
V(I / R _T ) = V(I / R₁ + I / R₂)
I / R _T = I / R₁ + I / R₂
R _T = R₁R₂ / R₁ + R₂

Therefore, total resistance for two resistors connected in parallel is given by;

Total resistance = Product of resistances / Sum of resistances

When resistors are connected in series, they give larger resistance than when connected in parallel. In parallel connection, each resistor has the same potential drop across it, and the currents through each resistor may be different depending on the resistance of a given resistor.
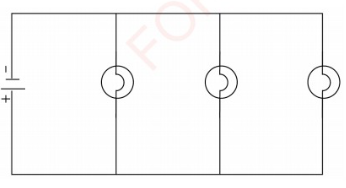
Note that, where bulbs have to be powered by a single source of electric current, the bulbs are connected in parallel (see Figure 2.25). This is practised in cars and home lighting systems. The advantages of a parallel connection over a series connection are:
1. The full p.d of source is applied across each bulb irrespective of the number of bulbs.
2. Switching one bulb on or off does not affect the others.



Activity 2.3
Aim: To study the flow current through bulbs connected in series and parallel.

Materials: Bulbs, bulb holders, ammeters, battery of 2 cells, switch, connecting wires

Procedure
1. Connect a battery to two bulbs arranged in series as shown in Figure 2.26.



2. Add a suitable ammeter by connecting it to the circuit as shown in Figure 2.27.



3. Switch on the circuit and note the ammeter reading.
4. Record your observations.
5. Open the switch, then move the ammeter to different positions within the circuit as shown in Figure 2.28.



6. Switch on the circuit and record your observations.
7. Remove one bulb from the series circuit and record the ammeter reading.
8. Now, connect the two bulbs in parallel as shown in Figure 2.29.



9. Add switches by connecting them to your circuit as shown in Figure 2.30.



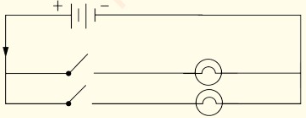
10. Switch on the circuit and record your observation.
11. Connect three ammeters to the circuit as shown in Figure 2.31, close the switches and record the readings.



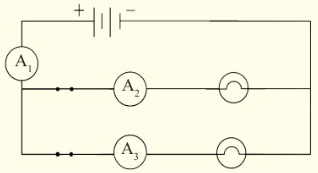
Do Activity 2.3

Questions
(a) What can you conclude about the current in steps 3, 6 and 11?
(b) How are the light bulbs in your home connected?

Example 2.4
Consider the circuit shown in Figure 2.32. If the p.d across the battery is 24 V, calculate the p.d across the 4Ω and 6Ω resistors.



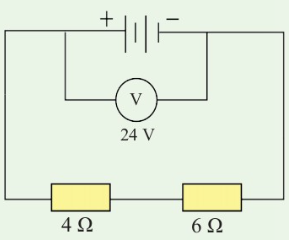
Solution
Total resistance in the circuit = 4 Ω + 6 Ω = 10 Ω
Using Ohm's law, I = V / R
Current in the circuit,
= 24 V / 10 Ω
= 2.4 A
Voltage across 6 Ω and 4 Ω
p.d across 6 Ω
V = IR
= 2.4 x 6
= 14.4 V

p.d across 4 Ω
V = IR
= 2.4 x 4
= 9.6 V

Therefore, p.d across 6 Ω and 4 Ω are 14.4 V and 9.6 V, respectively.

Exercise 2.2
1. Use information in Figure 2.33 to calculate:
(a) the p.d across the 5 Ω resistor.
(b) the current value across the resistor of 3 Ω.



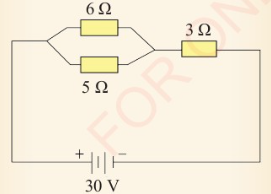
2. What is the difference between series and parallel circuit connection?
3. What is the p.d across the 2 resistor in Figure 2.34?



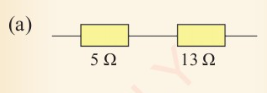
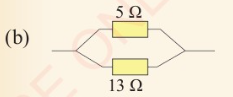
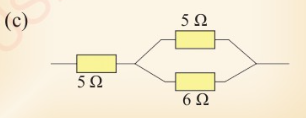
4. Calculate the combined resistance in Figure 2.35 (a), (b) and (c).







Chapter summary
1. Electric current is the amount of charge passing through a given point in a circuit per second.

2. Electric current is expressed as the rate of flow of electric charge, I = Q / t.

3. Electric current is one of the fundamental quantities and is measured in units of coulombs (C) per seconds (s) called amperes (A).

4. The direction of conventional current is opposite to the flow of electrons.

5. Electric current flows in all complete paths that allow it to return to its source. Electric circuits contain a source of moving electric charges such as a battery or a generator.

6. Resistors are used to control the flow of current and voltage in a circuit while obeying Ohm's law.

7. Ohm's law states that "at a constant temperature and other physical factors, voltage across the ends of a conductor is directly proportional to the current flowing through that conductor".

8. Resistance is the ratio of the potential difference across the ends of a conductor to the current flowing through that conductor.

9. The voltage is the amount of potential difference in an electric circuit.

10. Ammeters are connected in series to the source of electric charge while voltmeters are connected in parallel to the load and battery.

11. Total resistance for resistors in series is equal to the sum of individual resistances.

12. For any two resistors connected in parallel;
Total resistance = Product of resistances / Sum of resistances
That is;
R _T = R₁R₂ / R₂ + R₁
13. The amount of current in a circuit can be measured by using an ammeter.

Revision exercise 2
Choose the most correct answer in items 1-3.
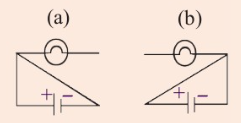
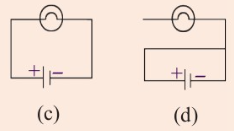
1. For a device in an electric circuit to work, the current must flow through it. Using Figure 2.36, select the circuit in which will light.





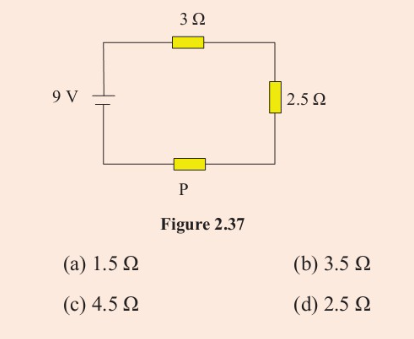
2. A current of 1.0 A passes in the circuit shown in Figure 2.37. What is the resistance of P?



3. The resistance of most metal conductors:
(a) increases with increasing temperature.
(b) increases with decreasing temperature.
(c) decreases with increasing temperature.
(d) decreases with decreasing temperature.

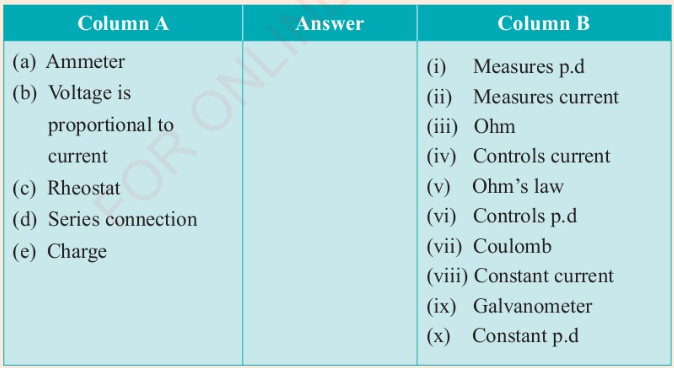
4. Match each item in column A against its corresponding item from column B by writing the correct response in the answer column provided.



5. (a) Explain the following concepts:
(i) electric current.
(ii) resistance.
(iii) voltage.
(b) Convert these currents into amperes:
(i) 500 µA.
(ii) 250 μA.

6. In an electric circuit, the current will flow along any complete path that allows the current to return to its source. In the circuit shown in Figure 2.38:
(a) Which bulb will light? why?



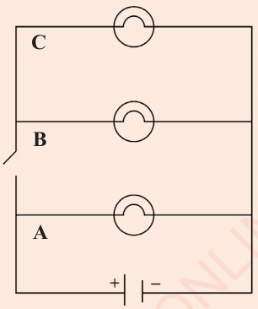
(b) Sketch the circuit in (a) and use arrows to show the direction in which the current flows.

7. Consider the circuit in Figure 2.39; (a) If bulb A burnt out, will bulbs B and C light up? Explain your answer.



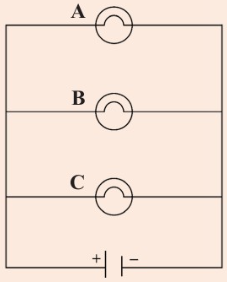
(b) Sketch the circuit in (a) and use arrows to show how the current will flow after bulb A burns out.

8. (a) Differentiate between potential difference and current.
(b) Using a diagram, show how an ammeter is connected to measure the current flowing through resistor, R.
(c) Draw a circuit diagram to show how a voltmeter is used to measure the potential difference of load, R.

9. (a) State Ohm's law.
(b) What is the SI unit of resistance ?

10. What could be the effect on the resistance of a conductor if:
(a) its length was increased?
(b) its temperature was increased?
(c) its cross-sectional area was reduced?

11. A current of 100 mA flows through a 5 k2 resistor. Determine the p.d across the resistor.

12. Three resistors of 2 2, 3 2 and 6 are connected in series to a 3 V battery. What is the current in the circuit?

13. (a) Two resistors of 6 2 and 12 are connected in parallel. Calculate their total resistance.
(b) Two resistors of 3 2 and 6 are connected in parallel.
(i) Draw the schematic diagram of the circuit.
(ii) Determine the total resistance of the circuit.
(iii) Calculate the p.d of the circuit when the current across it is 5 A.

14. Consider the circuit in Figure 2.40.



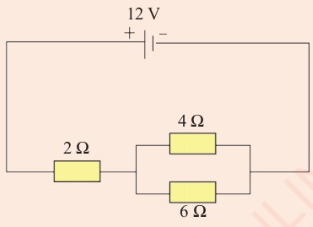
(a) Find the equivalent resistance.
(b) Determine the current in the circuit.

15. Suppose an additional 2 2 resistor is connected in parallel to the cell in Question 14.
(a) Draw the circuit diagram.
(b) Calculate the resistance of the circuit.

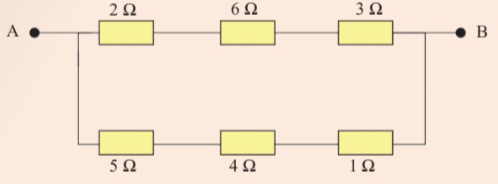
16. Basing on your observations in Activity 2.1, does adding an ammeter to a circuit affect the amount of current flowing? Explain your answer.

17. Two resistors of resistances 2 Q and 4 2 are connected to a Calculate the resistance of the circuit when:
(a) resistors are connected in parallel.
(b) resistors are connected in series.

18. Considering Figure 2.41, which one has a lower combined resistance?



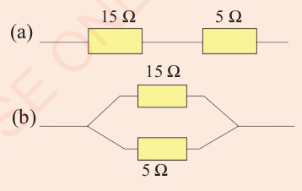
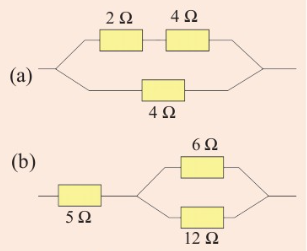
19. Calculate the combined resistance for each in Figure 2.42 (a) and (b).



20. Given two resistors, 4 and 6 2, and a battery, explain how you can connect them in a circuit.

21. If the p.d between points A and B in Figure 2.43 is 22 V, calculate the current between the points.