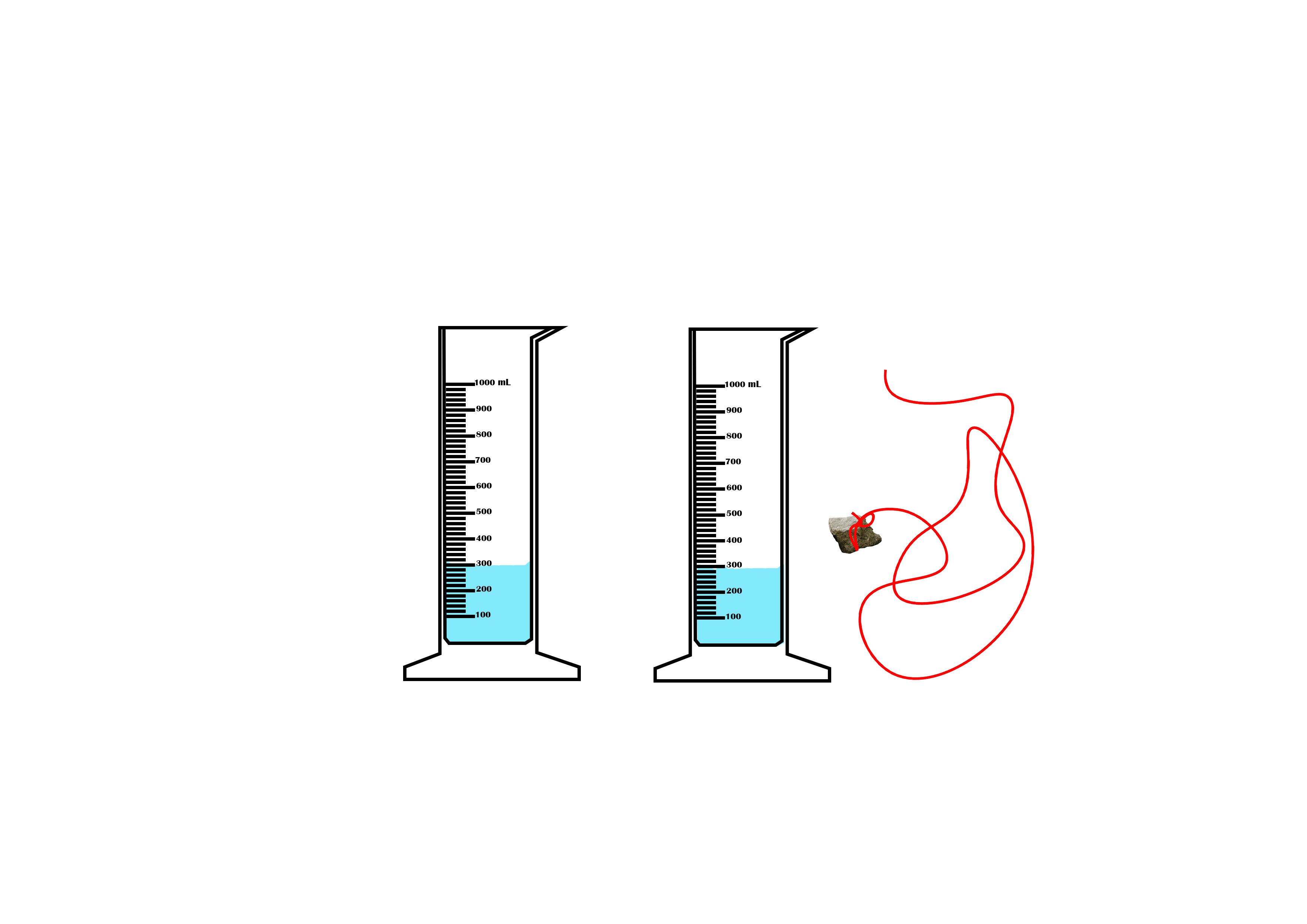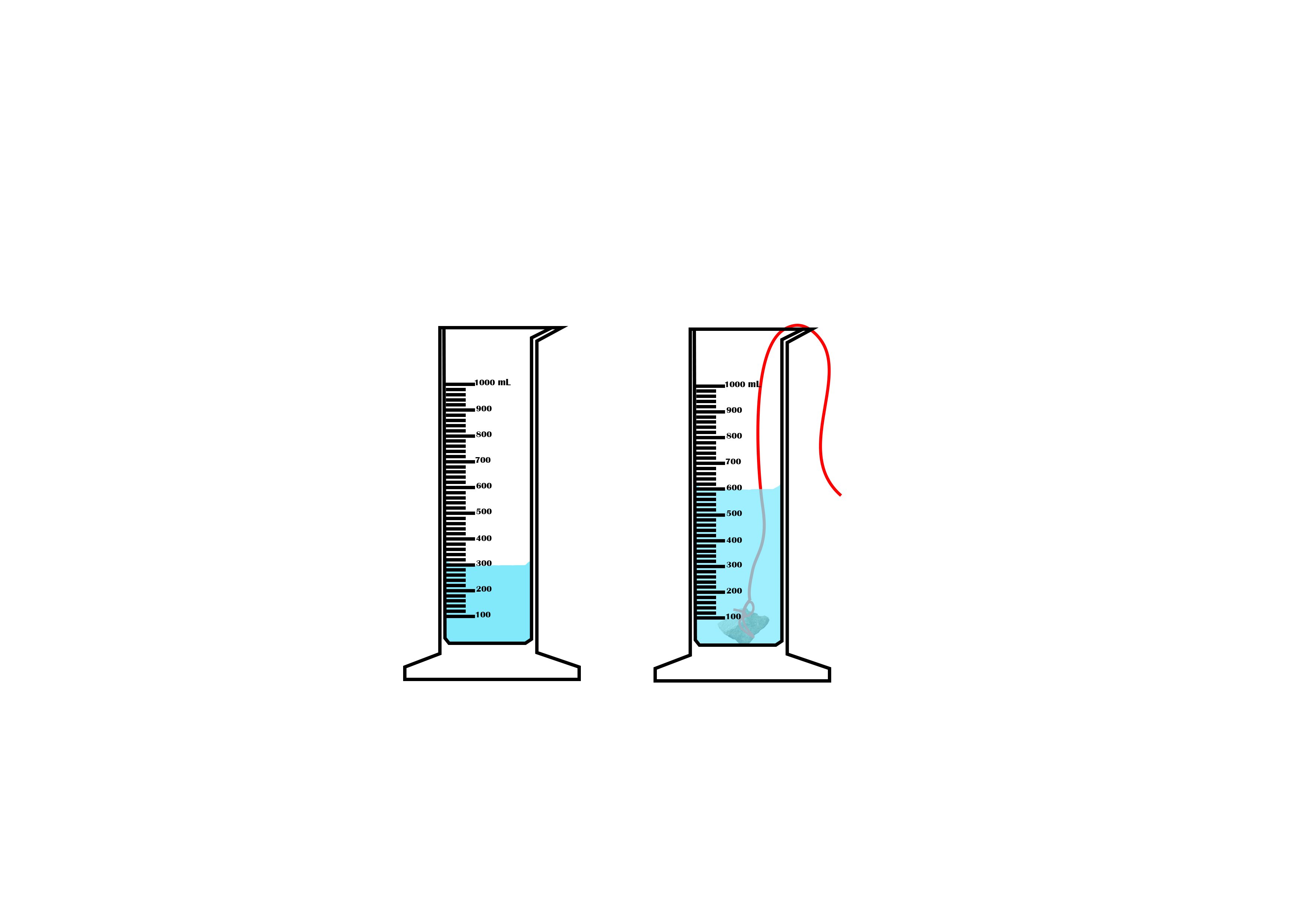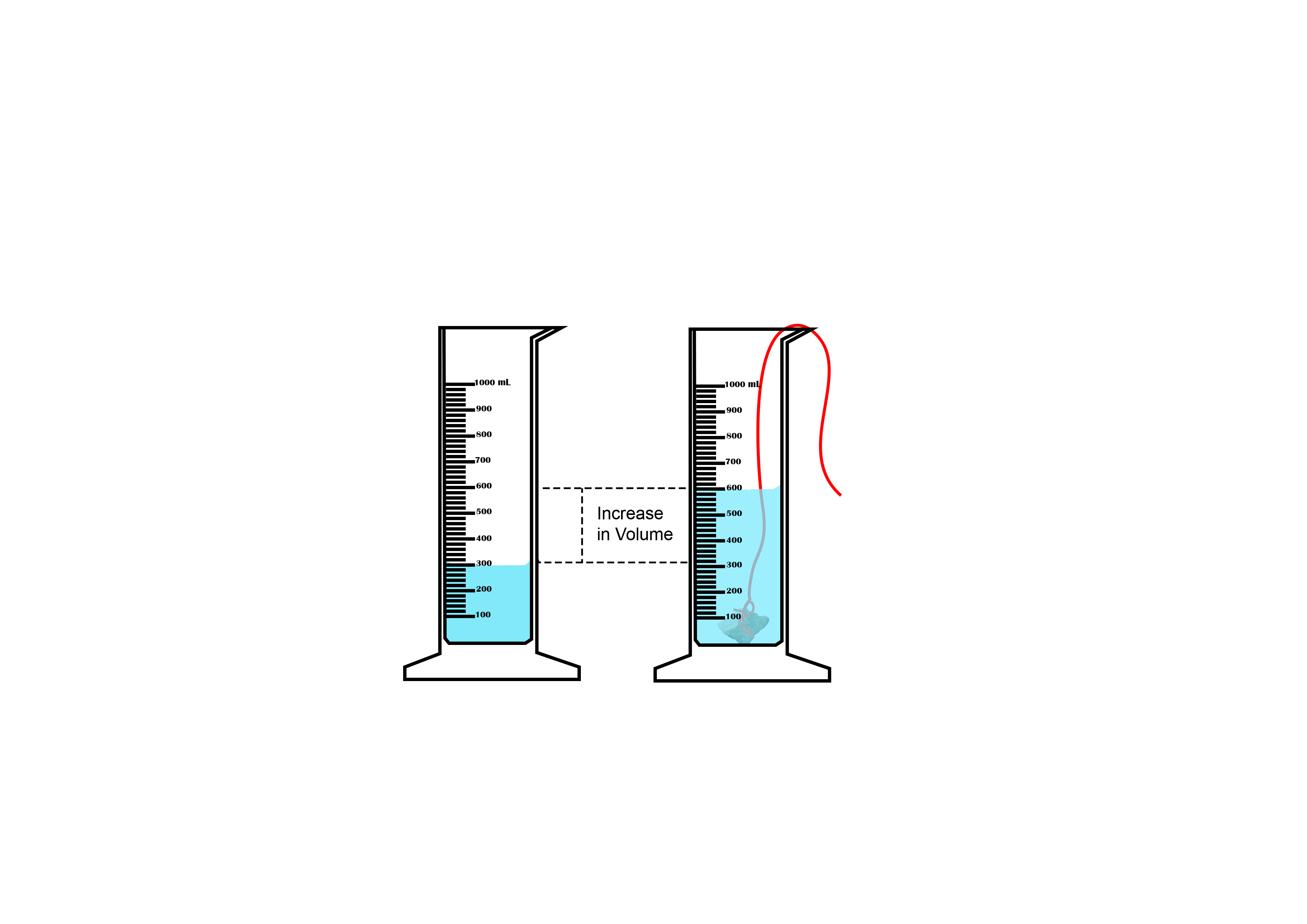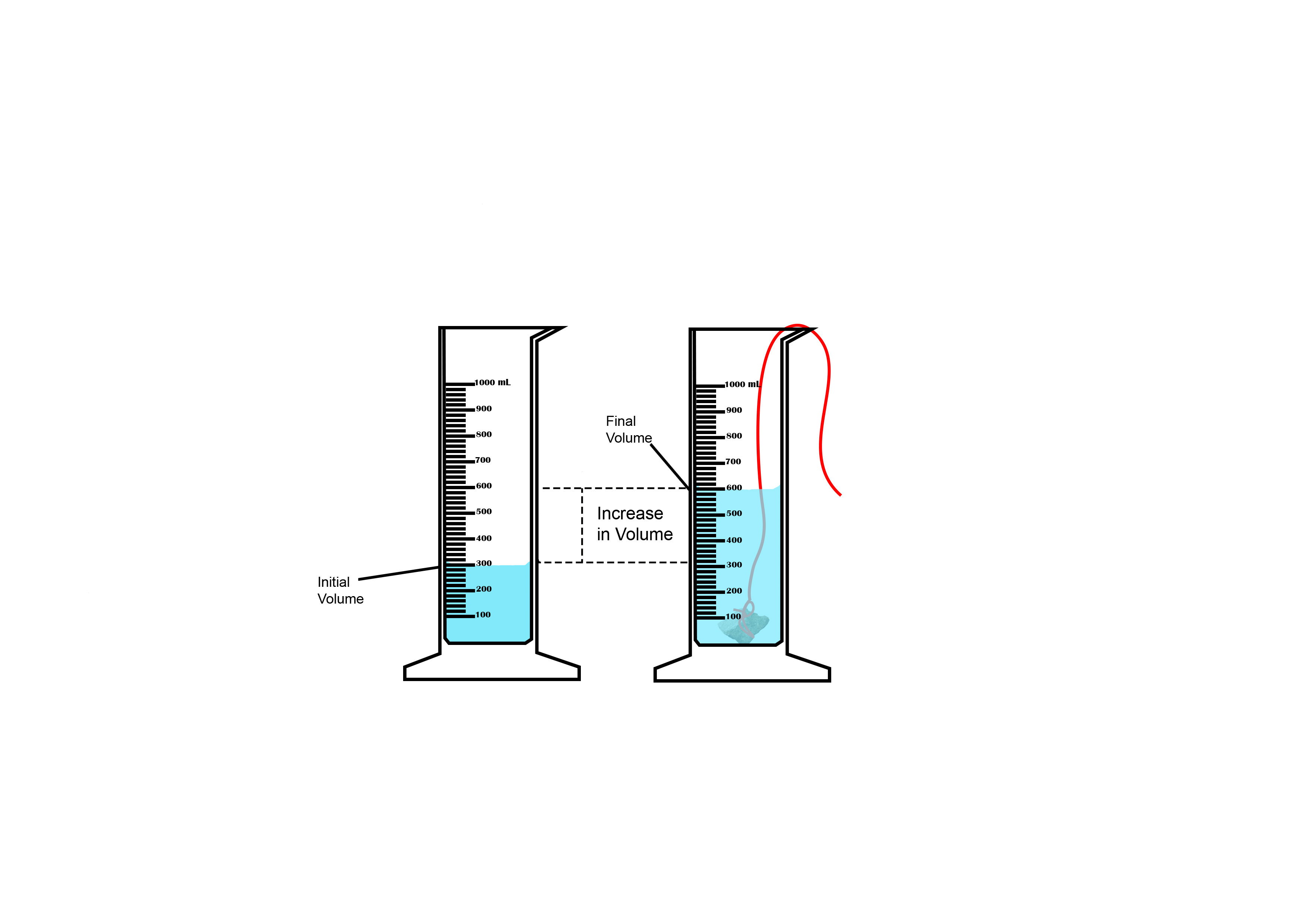The word 'measurement' comes from the Greek word 'metron' which means 'limited proportion'. It is our common experience that, if you want to buy a trouser, the information that a shopkeeper first wants to know is the size of the trouser that fits your waist. If it happens that you do not know your size, he or she will take a tape and measure the size of your waist. The act of finding the size of a given quantity is referred to as measurement.

Measurement is defined as the process of assigning a number and a unit to an observation or event. Measurement is done through comparing the known and unknown quantity. For example, in measuring the length of a table, we have to compare a table with a ruler or a tape measure.

Every measurement has two parts which are:
1. a number or numerical part that gives the result of the comparison; and

2. A unit part which identifies the particular unit used to make the measurement.

In the unit part, the focus is on the standard unit (International System Units-SI units) though, other units may also be used. For example, if the length of a playground is 100 m, '100' is the number part while 'm' is the unit part. Therefore, a meaningful measurement must have both a number and a unit.
A complete measurement which includes both number and unit part is called measurement of a physical quantity. For example, the measurement of 100 km, 2 kg or 10 s.

A physical quantity is any measurable quantity. Physical quantities are divided into two categories, namely fundamental physical quantities and derived physical quantities.

Fundamental physical quantities
Fundamental physical quantities are quantities of measurement which cannot be expressed in terms of other quantities. These include; length, mass, time, temperature, amount of substance, electric current and luminous intensity. Among the measured fundamental physical quantities mass, length and time are the most common. Table 3.1 shows the fundamental physical quantities and their respective SI units of measurement.

Table 3.1: The fundamental physical quantities and their SI units.



Vector and scalar quantities
The pysical quantities can futher be classified into either vector or scalar. quantities.

Vector quantities
Vector quantities are those quantities that have both magnitude and direction. Examples of vector quantities are force, displacement, velocity and momentum.

Scalar quantities
Scalar quantities are those quanties that have magnitude but have no direction. Examples of scalar quantities are mass, distance, time, density, volume, pressure, speed, electric current, work, energy, and power.

For example, consider a car travelling at 100 kilometres per hour North. This describes the velocity of the car which is 100 kilometres per hour in the North direction. Velocity is a vector quantity. However, if the intention is to describe only the speed of the car and not the direction, the statement could be simply that the car is travelling at 100 kilometres per hour. Speed is a scalar quantity.

Table 3.2 gives some of the vector and scalar quantities.

Table 3.2: Some of the vector and scalar quantities



Measurement of length
Length is the most commonly measured quantity in daily life. Length is used to give the dimensions of an object or the distance between two points. Hence, distance is defined as the path taken by a particle in space between two points or objects. The distance around the surface of an object is called perimeter. You can measure the distance ranging from very small to a very large distance such as the distance from the earth to the sun. To cope with this large difference, there are several other units obtained from the metre, namely, kilometre (km), centimetre (cm), millimetre (mm), micrometre (um), nanometre (nm), picometer (pm) and femtometre (fm). Their equivalence is as follows:
1 km = 1 000 m.
1 m = 100 cm.
1 cm = 10 mm.
1 mm = 1 000 µm.
1 μm = 1 000 nm.
1 nm = 1 000 pm.
1 pm = 1 000 fm.
Table 3.3 gives some of the units in comparison to the metre. Very small lengths are measured and expressed in mm, um, nm, pm or fm.
The length of an object is measured using specific instruments. The choice of an instrument to be used is determined by the following factors.
1. The desired degree of precision.
2. The size of the physical quantity to be measured.
3. The shape of the object.

Table 3.3: Gives some of the units in comparison to the metre.

Before you perform an experiment, you should be comfortable with equipment or apparatus that you will use. The following section describes some of the common ones and how to use them.

Equipment that are commonly used in a laboratory to measure length are a metre rule, tape measure, vernier caliper and micrometer screw gauge.

Metre rule
In an elementary physics laboratory, the metre rule, half-metre rule, and 30 cm rule as shown in Figure 3.1, are recommended to be used. These rulers are mainly wooden or plastic and are graduated in centimetres and millimetres. A typical metre rule has markings for 1 cm and 1mm intervals







Task 3.1
1. If you have to measure the length of a field, which type of instrument will you use?
2. Place the following objects on the paper. Mark the end points of each. Draw the line-segment for the length of each object and find the measure of length.
(a) A pencil
(b) A book
(c) A match stick

Tape measure
A tap measure, as shown in Figure 3.2, is a flexible ruler used to measure long Student's Book Form One distances and lengths of objects which are not straight. It is commonly used in civil work, for example in construction sites for houses, roads and bridges. It has the accuracy similar to the metre rule, with the minimum distance to be measured as 1 mm. Two basic types of tape measures are shown in Figure 3.2.





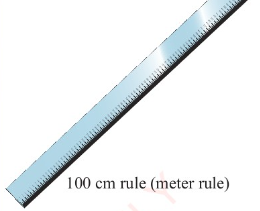
When taking a measurement, always ensure that your eye is perpendicular to the mark on the scale of the metre rule, as demonstrated in Figure 3.3, otherwise the value will have an error. An error caused by wrong positioning of the eye is known as parallax error. Such an error occurs when the measurement of an object's length is more or less than the true length, because of the eye being positioned at an angle to the measurement mark. Therefore, the eye should be perpendicular to the point you are reading, as shown in Figure 3.3.



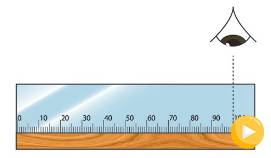
Care should be taken while using a metre rule so as to avoid damaging the ends. This is because the rule does not have an allowance (a short ungraduated portion) for wear at both ends. Suppose, you wish to measure the length of a table. The zero (0 cm) mark of the metre rule is aligned with one end of the table, as shown in Figure 3.4.



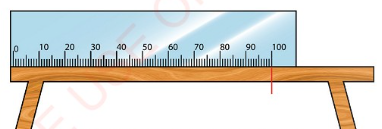
Since the metre rule does not extend beyond the end of the table, we carefully mark the point on the table that corresponds to the end of the metre and then continue, as shown in Figure 3.5.



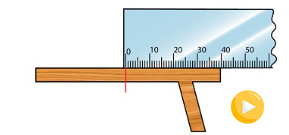
The actual length of the table is then given as: 100 cm + 40 cm 140 cm. Therefore, the table has a length of 140 cm or 1.4 m. In case the edge of a ruler is worn out, which is almost inevitable, it is advised to:

(i) always start measuring from the mark more than zero; and
(ii) subtract the mark from the final reading.

Figure 3.6 illustrates the use of a ruler with worn-out edges.



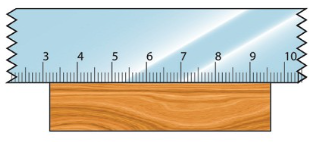
The length of the object = (9.6-3.2) cm = 6.4 cm.

Task 3.2
The following task should be carried out in groups of three students. Use a metre rule to measure the length and width of the cover of your physics textbook to the nearest tenth of a centimetre. Record your results. Calculate the perimeter of the cover. Perimeter = 2 times the length + 2 times the width = 2 (1+w). Present your results in the class.

A vernier caliper
A vernier caliper is an instrument used to measure small lengths with a greater degree of accuracy than a metre rule.

Measurement by use of a vernier caliper is obtained to the nearest hundredth of a centimetre, which means to the accuracy of 0.01 cm. A vernier caliper has a fixed scale and a vernier scale. The fixed scale is also known as the main scale. The vernier scale slides along the fixed scale hence readings are taken from both scales. The fixed scale gives readings in centimetres and millimetres while the vernier scale gives readings in the hundredth of a centimetre.
This explains the second decimal place. Figures 3.7 and 3.8 show a vernier caliper and a vernier scale for taking measurement.

Depth probe

main scale

main scale

vernier scale

inside jaw

outside jaw

outside jaw

vernier scale

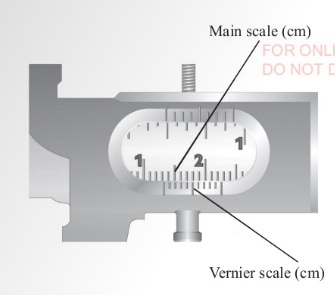
The vernier scale is a short scale. 10 vernier divisions cover 9 main scale divisions.
This is a length of 0.9 cm. When this is divided into 10 equal intervals, the result is the difference between the main scale division and the vernier scale division.
This is known as Least Count.
Main scale division = 1 cm / 10 = 0.1 cm.
Vernier scale division = 9 cm / 0.1 = 0.09 cm.
Therefore,
least count of a vernier caliper
= (0.1 -0.09) cm = 0.01 cm.

The vernier caliper has a set of 'jaws' that can be used to measure the lengths of some objects or the thickness of other objects.
They can also be used to measure the external diameters of objects using outside (outer) jaws, as shown in Figure 3.9.





At the top of a vernier caliper are two inner (upper) jaws that can be used to measure the internal diameter of a hollow objects, as shown in Figure 3.10. A stem sticks out from the right side of the caliper is called a depth gauge or a depth probe. It can be adjusted to measure a depth of an object, as shown in Figure 3.11.



The screw clamp visible on top of the caliper is tightened to secure the objects being measured, so that the reading does not change while measuring.

How to read a vernier caliper
The following steps are taken when measuring length using a vernier caliper.
1. Close the jaws of the vernier caliper and look out for the zero cm (0 cm) mark differences.
2. Place the object to be measured between the jaws.
3. Slide the vernier along the main scale until it just touches the end of the object. Use the screw clamp to secure the object in position, as shown in Figure 3.12.



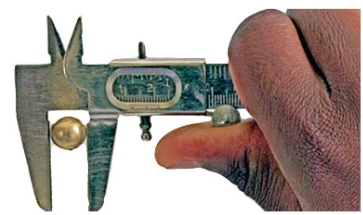
4. Read and record the reading on the main scale which is to the left of the zero cm mark of the vernier scale. This value is to the nearest tenth of a centimetre.
5. Observe along the vernier scale and record the mark which coincides with a mark on the main scale.
6. Read and note down the value on the vernier scale. This gives the digit in the hundredth place of the measurement.
7. Add the values in steps 4 and 6 to get your correct reading. Therefore, length of object = main scale reading + vernier scale reading.

Example 3.1
Using Figure 3.13, determine the diameter of the object that is placed between the jaws of the vernier caliper.



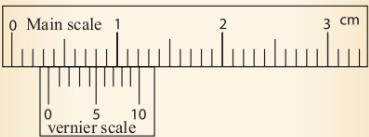
Solution
From Figure 3.13,
Main scale reading = 0.3 cm = 3.0 mm
Vernier scale reading = 5 divisions x 0.1 mm = 0.5 mm
Total reading = Main scale reading + Vernier scale reading
= 3.0 mm + 0.5 mm = 3.5 mm
Therefore, the total reading = 3.5 mm
The diameter of the object = 0.35 cm.

Example 3.2
The jaws of a vernier calliper touch the inner wall of calorimeter without pressure. The position of zero of vernier scale on the main scale reads 3.4 cm. The 6th of vernier scale division coincides with the main scale division. Vernier constant of callipers is 0.01 cm. Find actual internal diameter of calorimeter, when it is observed that the vernier scale has a zero error of - 0.03 cm.
Solution
Main scale reading = 3.4 cm
Least count (L.C) = 0.01 cm
Vernier coincidence = 6
Reading = Main scale reading + Vernier
coincidence x LC
= 3.4 + 6 × 0.01
= 3.4 +0.06
= 3.46 cm.
Corrected reading
= reading - zero error
= 3.46 - (-0.03)
= 3.54 +0.03
= 3.49 cm.

Exercise 3.1
Answer all questions
1. Draw both the main and vernier scales of a vernier caliper to show a reading of 0.36 cm.
2. What is the reading in Figure 3.14 (a) and 3.14 (b)?





3. The thin metallic strip of vernier caliper moves downward from top to bottom in such a way that it just touches the surface of a beaker. Main scale reading of calliper is 6.4 cm whereas its vernier constant is 0.1 mm. The 4th vernier scale division coincides with main scale division.
Calculate the actual depth of beaker. (Assume zero end error).

Activity 3.1
Aim: To measure the external diameter of a test tube using a vernier caliper.

Materials: Test tube, vernier caliper

Procedure:
1. Close the jaws of the vernier caliper and observe the zero cm marks of the main and vernier scales. Record your observations.

2. Open the jaws and place the test tube between them.

3. Close the jaws gently until the test tube is held firmly. Record your observations.

4. Repeat steps 1 to 3 using other parts along the test tube.

5. Obtain three readings. Record your observations.

Do Activity 3.1

Questions
(a) Calculate the average of the readings obtained.
(b) Were the four obtained readings equal?
(c) Explain why three readings were taken and not one.

A test tube is cylindrical in shape. This means that its diameter is the same throughout. The readings obtained using the outside caliper jaws are equal in magnitude since the test tube is almost uniform in shape.

In an experiment, it is always best to obtain many readings so as to obtain an average result. Two or more readings offer an opportunity for the experimenter to compare and identify any pattern.

Task 3.3
Collect a variety of objects such as books, pencils and other writing materials. In your collection, include cylindrical objects. Use a vernier caliper to measure the thicknesses of the collected objects. The depth, internal and external diameters of the hollow objects should also be measured. Record your measurements in the following table:



A micrometer screw gauge
A micrometer screw gauge gives readings with better precision than the vernier caliper.
Measurement can be obtained to the nearest thousandth of a centmetre. This is an accuracy of 0.001 cm. For this reason, it is usually used to measure the diameters of thin objects like wires and ball bearings. The micrometer screw gauge has different parts, as shown in Figure 3.15.

ratchet knob

Thimble

Sleeve(with main scale)

Anvil

Spindle (with rotating vernier scale)

Frame

View in your space

A micrometer screw gauge consists of main scale (sleeve) and thimble scale. The main scale is marked in millimetres. The thimble scale is divided depending on the distance between two consecutive threads of the screw. This is called the pitch of the screw. If the pitch of the screw of the micrometer is 0.5 mm, then the thimble scale has 50 equal divisions. Otherwise, it has 100 divisions when the pitch is 1.0 mm.
This means that when the thimble makes a complete turn, the spindle moves either forward or backward a distance of 0.5 mm or 1.0 mm respectively along the sleeve.
When the spindle is completely closed onto the anvil, the thimble edge aligns with the zero mark on the sleeve scale. The thimble also has its zero-mark lying on the central line of the sleeve scale. Therefore, the gap between the spindle and the anvil equals the distance between the edge of the thimble and the zero mark on the main scale.

To measure the diameter, an object is placed between the anvil and the spindle. The thimble is then rotated using the ratchet knob until the object is secured firmly between the anvil and the spindle. This in turn moves the spindle forward. The ratchet knob must be used to secure the object firmly, otherwise the instrument will be damaged or give a wrong reading. It is recommended that three clicks of the ratchet should be obtained before taking the reading. Note that as the thimble turns, it slides over the sleeve. The sleeve has a linear scale while the thimble bears a circular one. Care has to be taken to ensure that the thimble does not rotate while the reading is being taken.

Measuring the diameter of a wire by micrometer screw gauge
The following is the procedure for measuring the diameter of a wire using micrometer screw gauge.
1. Unscrew the thimble to create enough space to accommodate the wire between the spindle and the anvil.
2. Close the gap by rotating the thimble clockwise. Screw the ratchet knob until it clicks so as to show the correct setting.
3. Read and note down the value on the sleeve; that is the last mark must be visible to the left of the thimble. This value is to the nearest tenth of a millimetre. The value is 7.5 mm as shown in Figure 3.16.



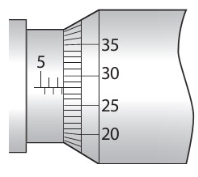
4. Read and note down the value on the thimble that is just below the reference line on the sleeve. This value is to the nearest hundredth of a millimetre (0.28 mm for Figure 3.16).
5. Add the values in steps 3 - 5. Therefore, for Figure 3.16,
Reading = Sleeve Scale Reading (SSR) + Thimble Scale Reading (TSR) Observed reading = SSR + TSR = 7.00 mm + 0.28 mm = 7.28 mm

Task 3.4
Diameter of a steel ball is measured using a vernier callipers which has divisions of 0.1cm on its main scale (MS) and 10 divisions of its vernier scale (VS) match 9 divisions on the main scale. Three such measurements for a ball are given as:



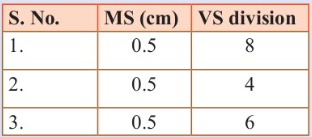
If the zero error is - 0.03 cm, calculate the average corrected diameter is:

Example 3.4
What is the correct reading for the micrometer screw gauges shown in Figure 3.17?





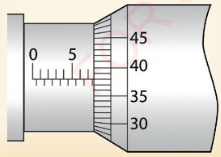
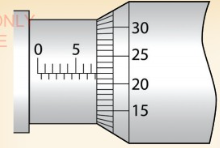
Solution
From Figure 3.17 (a)
(a) Main scale reading = 7.50 mm Thimble scale reading = 0.38 mm Reading = 7.88 mm.
From Figure 3.17 (b)
(b) Main scale reading = 7.50 mm Thimble scale reading = 0.22 mm Reading = 7.72 mm.

Example 3.3
When a screw gauge with a least count of 0.01 mm is used to measure the diameter of a rod, the reading on the sleeve is found to be 1.6 cm and the reading on the thimble is found to be 48 divisions. What is the correct diameter of the rod, if the zero error for the gauge is-0 003 cm?

Solution
Least count (LC) of a micrometer screw gauge given = 0.01 mm.
Main scale reading (MSR) = 1.6 cm or 16 mm.
Circular scale reading (CSR) = 48 divisions.
The reading = MSR + CSR x LC
The reading
= 16 mm + 48 x 0.01 mm = 16.48 mm
Correct reading
= 16.48 + 0.03 = 16.51 mm.

Exercise 3.2
Answer all questions
1. What is the reading of the micrometre screw gauge in Figure 3.18?



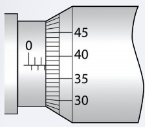
2. What is the difference between a micrometer having 100 divisions and one with 50 divisions?

3. State one limitation of using a micrometer screw gauge to measure length.

4. The actual diameter of a lead ball is 3.21 mm. Determine the reading that would have been obtained if:
(a) a micrometer screw gauge was used.
(b) a vernier caliper was used.

5. When a screw gauge with a least count 0.01 mm is used to measure the diameter of a wire, the reading on the sleeve is found to be 0.5 mm and the reading on the thimble is found to be 27 divisions. What is the correct diameter of the wire, if the zero error for the gauge is - 0 005 cm?

Activity 3.2
Aim: To measure the diameter of a steel ball using a micrometer screw gauge.

Materials: Micrometer screw gauge, steel ball

Procedure
1. Unscrew the thimble anticlockwise to create a gap between the anvil and the spindle.

2. Hold the steel ball in the gap while rotating the thimble clockwise until it gently grips the ball.
3. Turn the ratchet knob until it clicks.

4. Record your observations.

5. Unscrew the thimble slightly. Free the ball and turn it through a certain angle. Then repeat step 3.

6. Record your second observation.

7. Repeat step 5 and note the third observation.

Do Activity 3.2

Questions
(a) Calculate the average of the obtained readings.

(b) Why would you prefer a micrometer screw gauge to a vernier caliper in measuring this diameter?

A micrometer screw gauge is more accurate than a vernier caliper. It measures up to three decimal places in the unit of mm. This means that its degree of precision is to the nearest thousandth of a centimetre. Unlike a micrometer screw gauge, a vernier caliper can only measure to a hundredth of a centimetre.

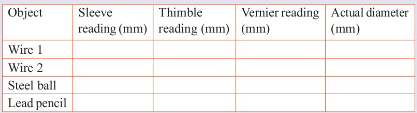
Task 3.5
Collect a variety of pieces of wire of different diameters, lead pencils and steel balls. In your groups:

1. Find out the smallest division on the main scale of your micrometer screw gauge and the number of divisions on the thimble.

2. Measure the diameters of the different objects. Each person in the group should measure at least one object. Record your findings in the following table.



Measurement of time
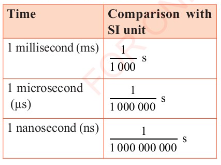
Time is a measure of the interval between two events, or the period within which an event takes place. It is the precise moment as determined by a clock or a watch. The SI unit of time is second (s). There are smaller units of time that are based on the second. These are the millisecond (ms), the microsecond (us), and the nanosecond (ns) as shown in Table 3.4.

Large units of time are minutes, hours, days, weeks, months and years as shown in Table 3.5.





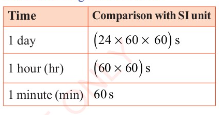
Reading time using stopwatch
Time is used to indicate when an event occurs, the order in which several events occurs or the rate at which an event happens. Under normal circumstances, time is usually measured using a clock or a wristwatch as shown in Figures 3.19(a) and (b), respectively.





For those experiments that require measurement of time in the laboratory, stopwatches are used. At this level, we shall concentrate on measuring time by means of a stopwatch.

A stopwatch is a device that is held in the hand and is used to show the time elapsed. Thus, the time interval is obtained from the time it is started to the time it is stopped. It is used when time must be measured precisely and with a minimum error. Stopwatches are used for timing laboratory experiments or sporting events like athletics.

There are two types of stopwatches, namely analogue stopwatch and digital stopwatch, as shown in Figure 3.20.

An analogue stopwatch has two scales, the minute scale and second scale. The pointer on each scale enables the time that has elapsed to be read, see Figure 3.20 (a).



A digital stopwatch shown in Figure 3.20 (b) displays the actual time in hours, minutes, and seconds. Digital stopwatches are more accurate than analogue stopwatches. A large digital version of a stopwatch is called a stop clock. Stop clocks are designed for viewing at a distance, such as in sports stadia.

How to operate a stopwatch
The timing functions of a stopwatch are controlled by two buttons, one at the top of the watch and the other to the side of the watch. Pressing the top button starts the timer and pressing it again stops the timer. The elapsed time is then displayed on the screen. The side button usually has two functions, first, to reset the stopwatch to zero and second to record the split times or lap times. When it is pressed while the stopwatch is running, the elapsed time is displayed, with the watch mechanism continuing to run to record the total time elapsed.

Activity 3.3
Aim: To determine the period of a simple pendulum.

Materials: , retort stand, analogue or digital stopwatch, object (200 g)

Procedure
1. With the guidance of your teacher, construct a simple pendulum by tying one end of the string to the retort stand.

2. Tie the 200 g object on the other end of the string.

3. Pull the object slightly to one side and release so that it swings back and forth.

4. Using a stopwatch, measure the time for the pendulum to swing back and forth ten times.

5. Record your observations.

6. Calculate the period (time for one complete oscillation).

7. Record your results.

8. Repeat steps 4-7 four times.

Do Activity 3.3

Question
Explain how you obtained the period (7) of the simple pendulum.

Measurement of mass
Mass is among the fundamental physical quantities of measurement. It is defined as the quantity of matter in an object. It measures the amount of matter in an object.
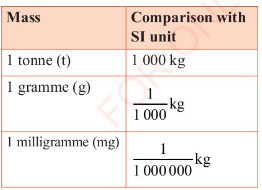
The SI unit of mass is the kilogramme, written as kg. Other units of mass based on kilogramme are tonne (t), gramme (g) and milligramme (mg). Their equivalences are as given below. See also Table 3.6.
1 tonne = 1 000 kg.
1 kilogramme = 1 000 g.
1 gramme = 1 000 mg.



Mass should not be confused with weight as is evidenced in day-to-day discussions and conversations. Weight is defined as a measure of the gravitational force acting on an object, or is the measure of how heavy an object is.

Measurement of mass using different instruments
The equipment commonly used to measure the mass of an objects in the laboratory is digital (electronic) balance, shown in Figure 3.21 (a), or triple beam balance shown in Figure 3.21 (b).





A triple beam balance
A triple beam balance shown in Figure 3.21 (b) is used to measure the mass of an object. Its unit of measurement is the gramme.
It is called triple beam balance because it contains three beams, each with specified standard mass graduations or markings.
The first beam has 100 g graduations, the second has 10 g graduations while the third beam has 1 g graduations with 0.1 g graduations in between. To measure the mass of an object, the weights which are normally attached to each beam, are moved along the beams.

How to use a triple beam balance (Depends on the mass)
1. With the pan empty, move the three weights to the left of the beams, so that the balance reads zero, as shown in Figure 3.22. The balance pointer should be straight and aligned with the fixed mark at the right of the balance. If the pointer is not straight, use the counter weight to adjust as needed.



2. Once the balance has been adjusted, place the object to be measured on the pan.

3. Move the 100-gram weight to the right along its beam until the indicator just drops below the fixed mark. The mark to the immediate left of this point indicates the number of hundreds of grams. Note down this value which is 0 for the case of Figure 3.23.

4. Move the 10 gram weight to the right along its beam until the indicator drops below the fixed mark. The mark immediately to the left of this point indicates the number of tens of grams. Note down this value, 20 for the case of Figure 3.23.

5. Move the 1 gram weight to the right along its beam until the pointer coincides directly with the fixed mark on the right, as shown in Figure 3.23. Note down this value which is 5 and given to the nearest tenth of a gram.



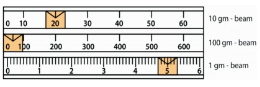
6. To find the mass of the object on the pan, add the numbers from the three beams. That is, 0g + 20 g + 5 g = 25 g

Example 3.5
The diagram in Figure 3.24 shows the position of the three weights on the beams of a triple beam balance. Determine the mass of the object.



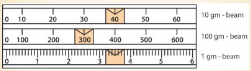
Solution
We start with 100 g, 10 g, then 1 g. That is, 300 g + 40 g + 3.5 g = 343.5 g.

A digital balance
A digital balance shown in Figure 3.21 (a) is a very sensitive weighing balance. It can measure masses to an accuracy of one thousandth of a gram (0.001 g).
The object whose mass is to be measured is placed on the pan on top of the balance and the mass read from the digital display.

Task 3.6
In your regular discussion groups, carry out the following:
1. Use a triple beam balance to measure the mass of your physics textbook, exercise book and your pen.

2. Use a digital balance to measure the mass of the same materials.

3. Compare the two measurements and discuss any differences.

Exercise 3.3
Answer all questions
1. Differentiate between estimated length and measured length.

2. State three basic fundamental quantities of measurement and their SI units.

3. Explain how the following fundamental physical quantities can be measured:
(a) Length.
(b) Mass.
(c) Time.

4. Differentiate between the following items:
(a) A stopwatch from a stopclock.
(b) An analogue from a digital stopwatch.
(c) Mass from weight.

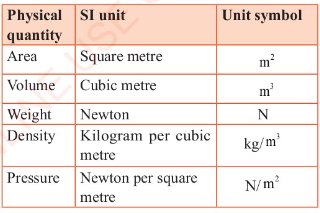
Derived quantities are obtained by combining the fundamental quantities through the application of basic arithmetic operations, namely multiplication and/or division. Their units are called derived units and the same method is used in deriving them. Examples of derived quantities are area, volume, density, velocity and acceleration. Their derived units are m², m³, kg/m³, m/s and m/s², respectively, as shown in Table 3.7.



These quantities are calculated using certain formulae or they are determined experimentally. For example,
Area (4) of a square = length (1) × length (1) = 1 × 1 = P.
The SI unit of area is the square metre, m². However, areas of other regular shapes are calculated using Student's Book Form One their respective formulae depending on the shape of the object. This will be learnt more in mathematics lessons, though a few of them will be discussed in this textbook.

Measurement of volume
Volume is the quantity of space that an object occupies. The SI unit of volume is cubic metre (m³). One cubic metre is the volume of a cube with sides 1 m long. Other units of volume includes:
(a) cubic centimetre (cm³);
(b) millilitre (ml); and
(c) litre (1).
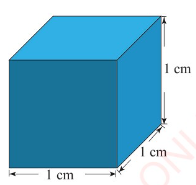
The cubic metre is rather a large unit of volume for everyday school laboratory work. For convenience purposes, volumes are measured using the cubic centimetre (cm³). One cubic centimetre is the volume of a cube with sides 1 cm long, as shown in Figure 3.25.



Techniques for measuring volume
The techniques for measuring volume do vary depending on whether the sample is liquid, solid, or gas.

Liquids
Litre is another unit used for measuring the volume of liquids.
1 litre (1) = 1 000 cm³= 1 000 ml. This implies that 1 cm³ = 1 ml. The volume of water in a 1- litre = 1 / 1 000 m³ as shown in Figure 3.26.



Several graduated apparatus such as a graduated cylinder, burette or pipette are usually used to measure the volume of a liquid in the laboratory. Calibrated beakers and flasks can also be used. In rare cases, syringes are used for measuring the volume of liquids. A burette, a pipette or a volumetric flask gives accurate measurement of liquid volumes.

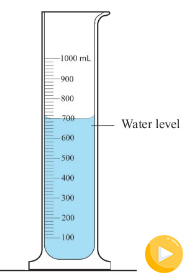
Measurement of volume using a measuring cylinder
Graduated measuring cylinders are used to measure the volume of a liquid, ranging from a few millilitres to hundreds of millilitres. They are of different sizes, made of glass or plastic. Measuring cylinders are graduated from the bottom upwards. They measure the volume of liquids that are poured into them. An example of a measuring cylinder is shown in Figure 3.27.



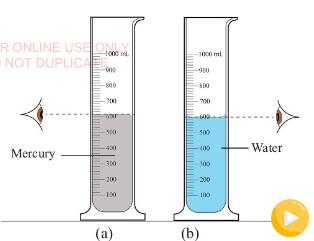
When reading a measuring cylinder, the cylinder must be placed on a level surface.
The curve in the upper surface of the liquid is called the meniscus. The meniscus can curve upward (concave) or downward (convex) depending on the liquid and the material of the cylinder. The volume of the liquid is read at the top of the meniscus or at the bottom of the meniscus, as illustrated in Figure 3.28 (a) and 3.28 (b), respectively. Note that the eye level should be in line with the meniscus of the liquid.





Task 3.7
Carry out the following task in groups of four students. Fill a drinking cup with water and then pour the water into a graduated measuring cylinder.
Measure the volume of water and record. What is the reading on the cylinder?

Measurement of volume using a burette
A burette is a vertical cylindrical piece of laboratory glassware with a volumetric graduation on its full length and a precision tap, or stopcock on the bottom, as shown in Figure 3.30. It is used to dispense a required amount of a liquid reagent for which high precision is desired. A burette is graduated from the top downwards and measures the volume of a liquid that runs out from it.
The use of a burette involves the following steps:
1. Pour the liquid into the burette and make sure that it does not pass the 0 mark at the top. Note down this volume, say V₁.

2. Note down the value of the amount of liquid you require to use, say V and add it to V, to get V₂

3. Open the tap and let the liquid runs until the level of the liquid reaches V₂.

4. Subtracting V, from V₂ gives V.



Measurement of volume using a pipette
A pipette is a glass or plastic tube, usually open on both ends. A pipette is shown in Figure 3.31. It is used to transfer a known amount of a liquid from one container to another. The liquid is sucked into it until it reaches the level of the mark shown.



Sometimes a flexible rubber bulb is placed at one end of the pipette to aid in sucking the liquid from a container, as shown in Figure 3.32.



Common laboratory pipettes are calibrated with 20 cm³, 25 cm³ or 50 cm³. The 20 cm³ pipette is used to measure 20 ml of liquid while the 25 cm³ and 50 cm³ pipettes are used to measure 25 ml and 50 ml of liquid, respectively. This shows that pipettes are specifically made for transferring small amounts of liquids only from one container to another.

Activity 3.4
Aim: To measure volume of water using a pipette.

Materials: Pipette, beaker, graduated cylinder, water

Procedure
1. Pour 100 ml of water into a beaker.

2. Transfer 25 ml of water from the beaker to a graduated cylinder using a pipette.

3. Observe the meniscus of the water in the cylinder and record its reading.

4. Record the volume of water in the graduated cylinder.

Do Activity 3.4

Questions
(a) Compare the original volume of water in the pipette with the volume of water in the cylinder and state your observations.
(b) Is the volume of water transferred from the beaker equal to reading in the cylinder? Explain.
(c) Discuss your findings.

The volume of water transferred into the measuring cylinder equals the volume of the pipette. This is because the volume of a liquid does not change, irrespective of the apparatus used.

Measurements of a volume of a solid
(a) Determining the volume of regular objects
Dimensions of a solid with regular shape such as a cube, a cylinder or a sphere, can be measured and the appropriate formula is used to calculate its volume.
For example;
Volume (V) of a rectangular block = length (I) height (h) x width (w). For a cube, I = h = w,
Volume of a cylinder
= π × (radius,r)² × (height, h) = πr² h
Volume of sphere = 4 / 3 πr²

Example 3.6
Calculate the volume of a rectangular block, of sides 15 cm, 8 cm and 7 cm, as shown in Figure 3.33.

Solution



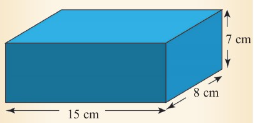
Volume of the block = l × w x h
= 15 cm x 8 cm x 7 cm = 840 cm³.

Example 3.7
Calculate the volume of the cylinder shown in Figure 3.34, given that π = 3.14.



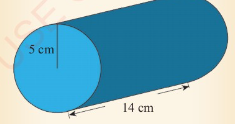
Solution
Given, π = 3.14, r = 5 cm and 1 = 14 cm Formula for calculating volume of a cylinder V = πr²l
Substituting in the formula gives,
V=3.14 x 5 cm x 5 cm x 14 cm = 1099 cm³.

(a) Determining the volume of irregular solid objects
Measuring the volume of an irregular shaped solid object is based on the Archimedes' principle which states that 'when an object is completely submerged in water, it displaces a volume of water equal to its own volume'. The displacement or immersion method is used.
The volume of an irregular object can be measured using:
(a) a measuring cylinder; and
(b) eureka can or an overflow can.

Volume of irregular object by using a graduated cylinder
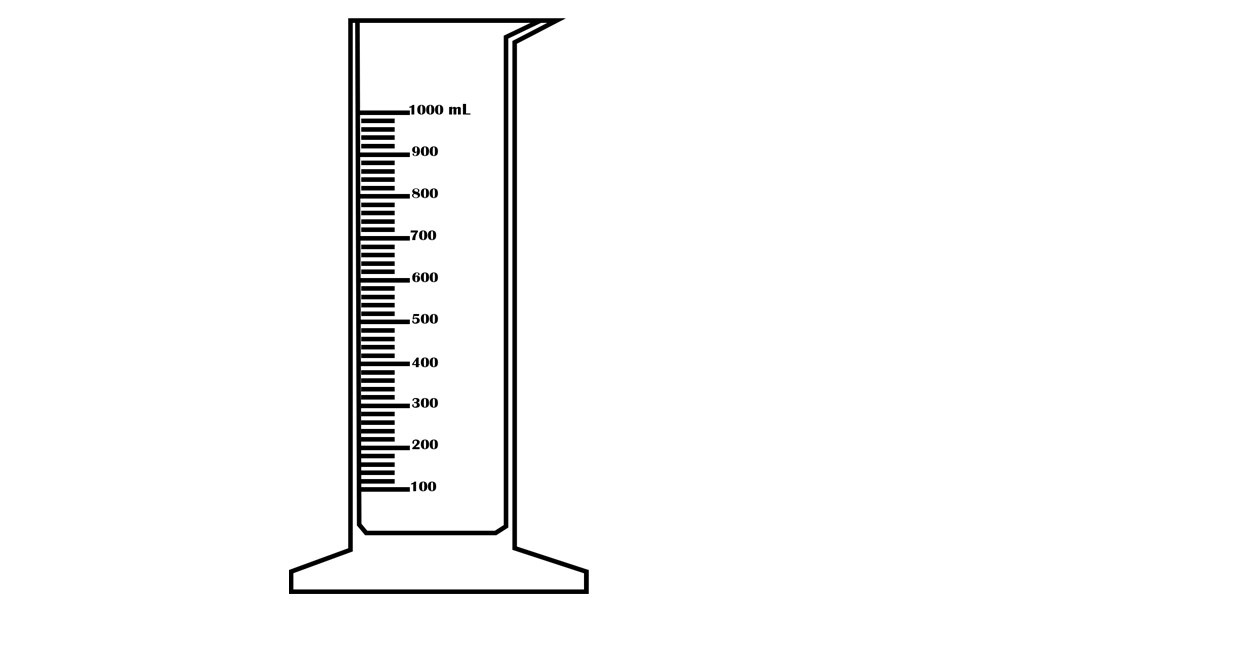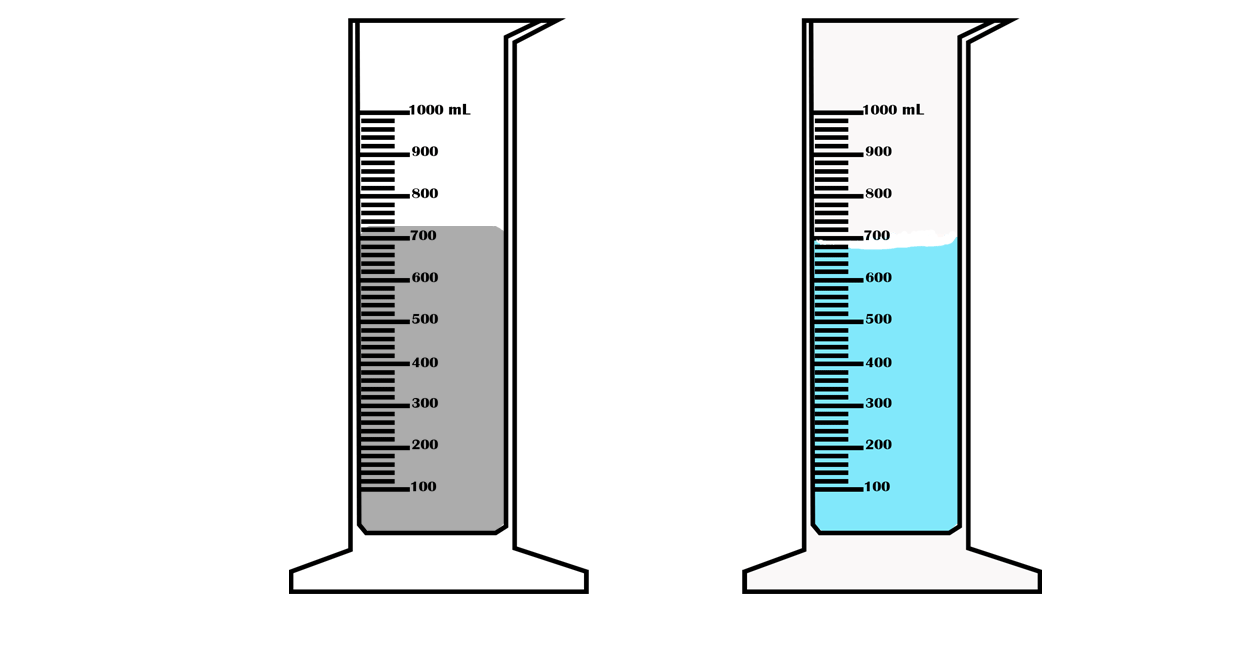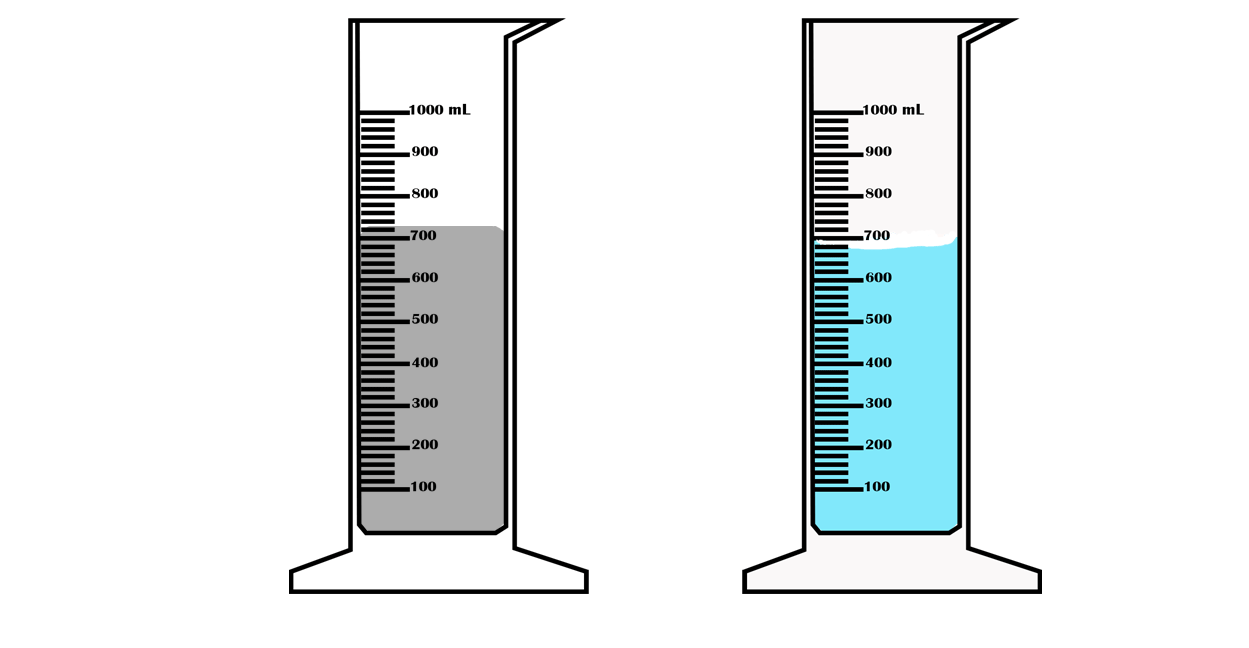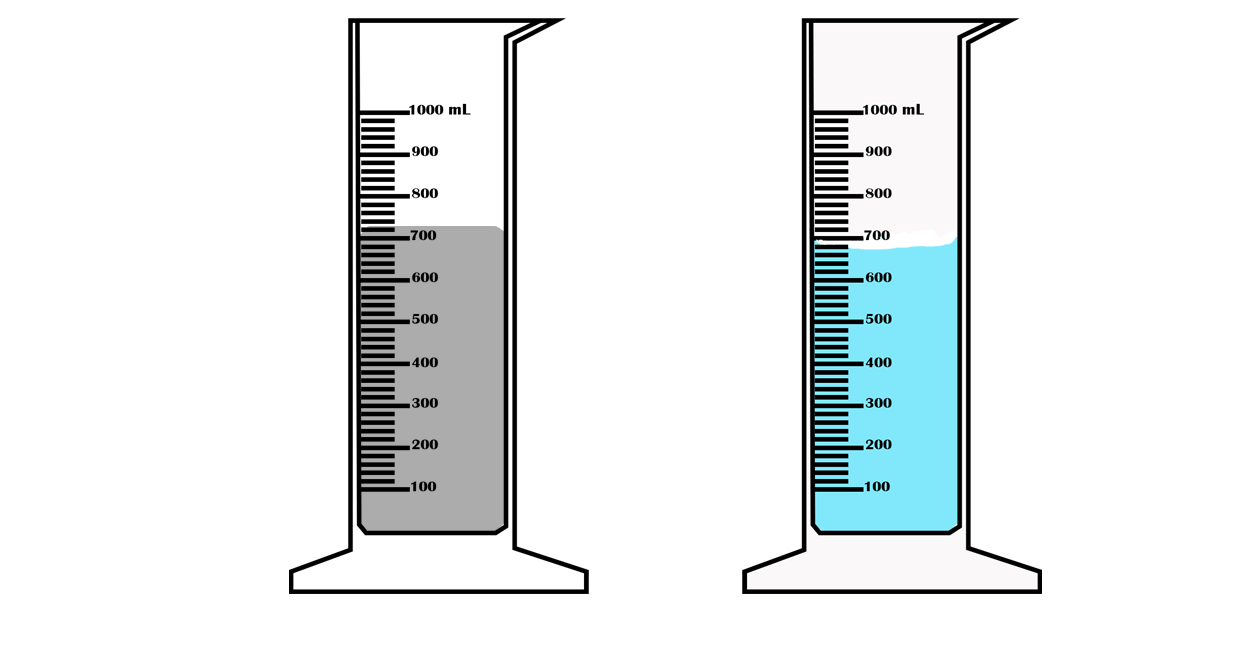
Suppose you want to measure the volume of a small stone.

The following steps are necessary.
1. Fill a graduated cylinder with about 300 ml of water as shown in Figure 3.35 (a).

2. Carefully measure the initial volume of water V₁.

3. Then gently lower the stone into the water as shown in Figure 3.35 (b).

4. Read the final volume of water V₂.

5. The difference between the final and the initial volume gives the volume of the stone.
Volume of the stone (V _s )
final volume (V₂) - initial volume (V₁)
V _s = V₂ - V₁.



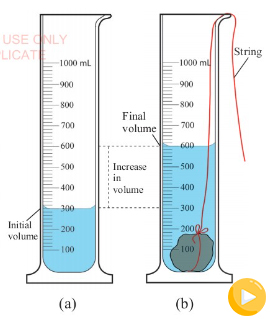
In the illustration,
V _s = 600 ml - 300 ml = 300 ml.

Example 3.8
When an irregular solid object was immersed in 65 cm³ of water, the water level rose to 81 cm³. What was the volume of the irregular solid object?

Solution
Initial volume of water V₁ = 65 cm³
Final volume of water V₂ = 81 cm³
Using volume of solid, V = V₂ - V₁
gives
V _s = 81 cm³ - 65 cm³ = 16 cm³
Therefore, the volume of the irregular solid is 16 cm³.

Volume of an irregular objects by using eureka can
If the object is too large to fit into the graduated cylinder, an alternative method is to use an overflow can commonly known as a eureka can as shown in Figure 3.36.
This is a large can with an overflow spout near the top. In practice, the following steps are involved when using an overflow can to measure the volume of an irregular object.
1. Fill the eureka can with water up to the level of the spout.



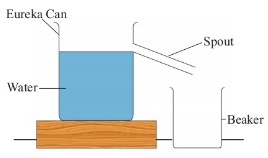
2. Tie the irregular object with a string.

3. Gently lower the object into the water using the string.

4. The object will displace some water which will be collected in the beaker, as shown in Figure 3.37.



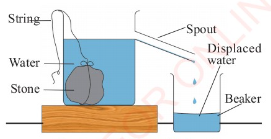
5. Transfer the displaced water into a graduated cylinder, as shown in Figure 3.38.

6. Measure the volume of the displaced water which is equal to the volume of the object.



Note: Hence, the volume of solid objects with irregular shape can be determined by using immersion methods.

Activity 3.5
Aim: To measure volume of an irregular object using a eureka can.

Materials: eureka can, stone, water, beaker, graduated cylinder, string



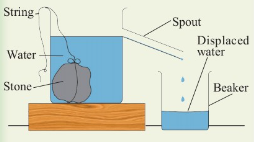
Procedure
1. Set up the apparatus as in Figure 3.39.

2. Tie the stone with a string and gently lower it into the water contained in the eureka can.

3. Collect the overflowing water in the beaker below the spout.

4. Measure and record the volume of the displaced water using a measuring cylinder.

5. This volume is equal to the volume of the stone.

Do Activity 3.5

Questions
(a) Why must the stone be tied and gently lowered into the water?
(b) Why is the water in the eurica can displaced when the stone is immersed?

The stone is tied before lowering it so as to prevent water from splashing. This would give wrong results as the remaining water level would be lower than the spout level.
It would also interfere with the volume to be measured. The water is displaced so as to give room for the stone. The stone occupies a volume which is equal to the volume of water displaced.
If the solid has an irregular shape such as a stone, it is submerged in a measuring cylinder containing water and the volume of water displaced is taken as the volume of the solid.

Determination of volume of gases
A gas always fills any container into which it is placed. Therefore, the volume of a gas can be determined by measuring the Student's Book Form One volume of the container into which it is put. The volume of the container can be determined from its dimensions or by filling it with water and then pouring the water into a graduated cylinder.

Exercise 3.4
Answer all questions
1. Calculate the volume of a cube of sides 2 cm.

2. The volume of a brick is given as 60 cm³. Given that its length and width are 6 cm and 4 cm respectively, calculate its height.

3. A cylindrical container has a diameter of 10 cm and a height of 12 cm. Calculate its volume, given that π = 3.14.
4. A beaker contains 100 cm³ of liquid. A 25 cm³ pipette is used twice to transfer the liquid to another beaker. What is the volume of the liquid left in the original beaker?

5. The initial volume in a burette was read as 80 cm³. X cm³ of the liquid was run out and the final volume was read as 57 cm³. Calculate the value of X.

6. What is the volume of an irregular solid immersed in 50 cm³ of water contained in a beaker if it raises the water level to 57 cm³.

While taking any measurement, there may be some error in the reading. An error is defined as a deviation from the actual reading. However, there is a more precise definition. An error is a measure of estimated difference between the measured value and the actual value of a physical quantity that is being measured or observed. Errors usually arise due to several reasons:

1. Fault during manufacture - If a measuring instrument is not manufactured as per specification, then the accuracy is lowered.

2. Damage during use - Bad handling of instruments can lead to incorrect results. Each apparatus should be used properly and for the right purpose.

3. Poor storage-Apparatus should be well stored away from factors that affect their accuracy like dust and heat.

4. Human factors - Errors can arise when an experimenter does not take readings from an instrument properly. The three common errors due to improper reading of an instrument are:
(i) Parallax error;
(ii) Zero error; and
(iii) Instrumental error.

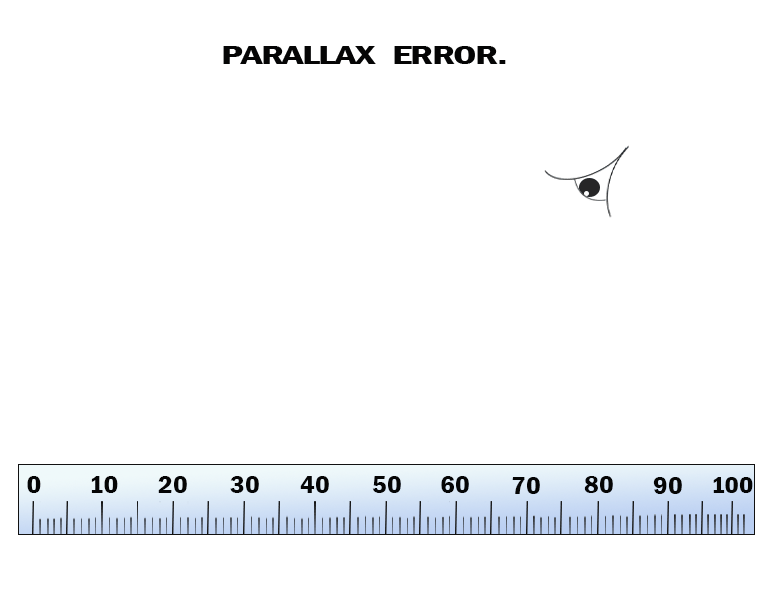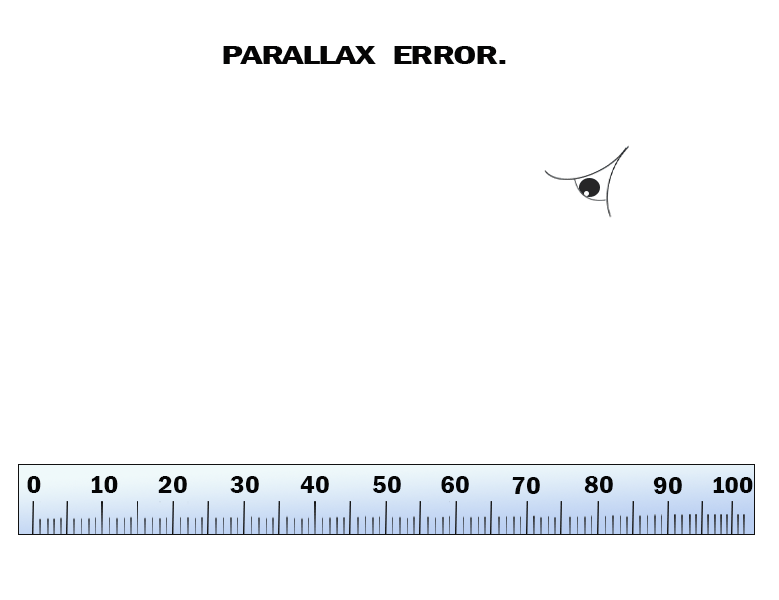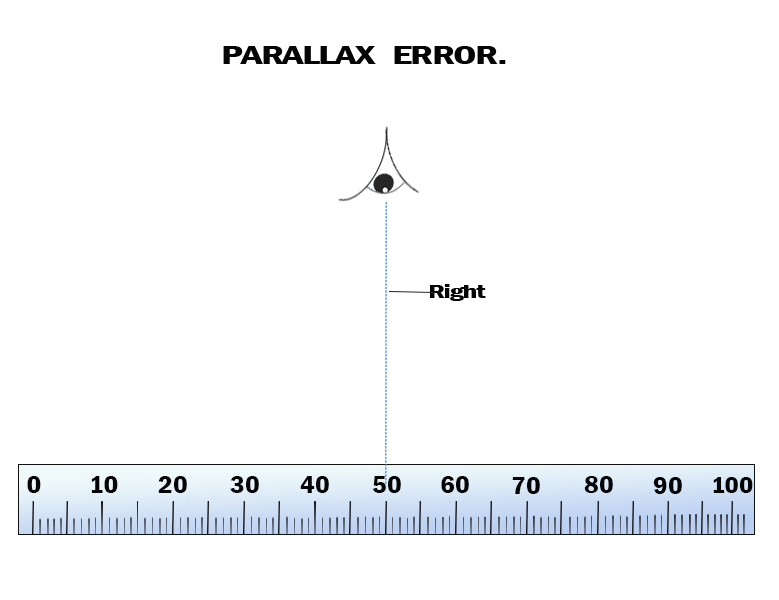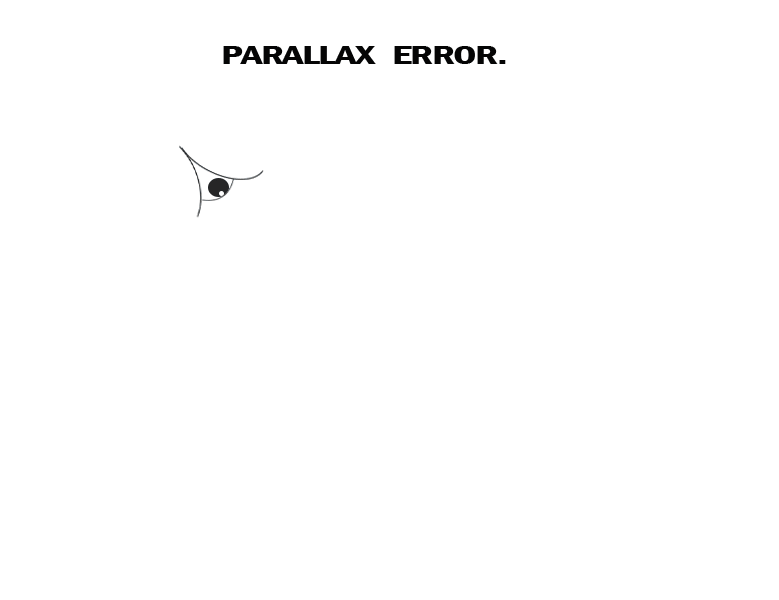
Parallax error
Parallax error occurs when an observer takes measurement from wrong positions. Consider Figure 3.40.



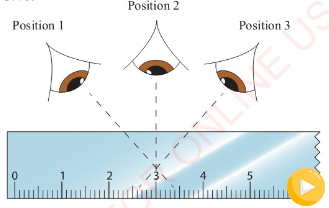
Positions 1 and 3 will give higher and lower readings than position 2. A reading taken at position 2 will be correct because the observer has positioned his/her eyes directly above the mark to be read. To minimize parallax error, the observer must position his/her eyes directly above the mark to be read.

Zero error
For a measurement to be considered accurate, the initial reading of a pointer should be at a zero mark.





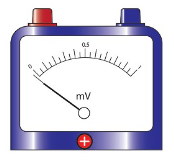
When a measurement is taken with an instrument with the pointer below or above the zero mark as shown in Figure 3.41 (a) and Figure 3.41 (b), zero error is said to occur.
To minimise zero error, the instrument should be adjusted to read zero, as shown in Figure 3.42. A pointer can be adjusted to read zero.



For example, in a vernier caliper, zero error arises when the zero mark on the main and vernier scales do not coincide with each other when the jaws are closed. A micrometer screw gauge may also have zero error if the zero marks on the spindle and sleeve do not coincide after closing the gap between the spindle and the anvil.

Instrumental error
An instrumental error is caused by an instrument itself. The error occurs because of defects in the instrument used in taking a measurement. These defects can be from the manufacturer or they may result from poor handling of the instrument. Sometimes errors of this type may occur when the instrument used for measuring is overheated. Also, insensitivity of the instrument can result in this error. To minimise these errors, avoid overheating instruments, maintain them regularly and store all instruments in a safe place free from dust. Proper handling of instruments is also recommended.

Chapter summary
1. Initially, approximations were used as a form of measurement. Advancement in science has made it possible to have appropriate instruments for each type of measurement.
2. Every measurement has the number part and the unit part. This complete measurement is called measurement of a physical quantity.
3. Fundamental quantities are the physical quantities which cannot be . obtained from any other quantities. These quantities include length, mass, time, temperature, amount of substance, electric current and luminous intensity.
4. The three fundamental quantities of measurement are mass, length and time. Their SI units are the kilogramme, metre and second, respectively.
5. The beam balance and digital balances are used to measure mass, while rulers, vernier calipers, micrometer screw gauges and tapes are used to measure length. On the other hand, time is measured using a stopwatch or a clock.
6. Derived quantities are obtained by dividing or multiplying two or more fundamental quantities. These quantities include weight, acceleration, velocity, volume and area. Their SI units are the Newton, metre per second square, metre per second, cubic metre, and square metre, respectively.
7. There are three types of errors that emerge during measurements, namely:
(a) parallax error;
(b) zero error; and
(c) instrumental error.

Revision exercise 3

Section A
Choose the most correct answer
1. To measure the length using a metre rule, wrong position of the eye leads to:
(a) parallax error.
(b) eye error.
(c) zero error.
(d) metre error.

2. Which of the following instruments is most suitable for measuring the internal diameter of 100 ml beaker?
(a) Metre rule.
(b) Vernier caliper.
(c) Measuring tape.
(d) External caliper.

3. The mass of an object is reduced if its
(a) state is changed.
(b) amount of matter is reduced.
(c) surface is reduced.
(d) volume is reduced.

4. A cuboid with length 3 cm, width 4 cm and height 10 cm is made from wood. The actual volume of the cuboid is
(a) 120 cm³.
(b) 240 ml.
(c) 120 m³.
(d) 240 cm³.

5. What is the zero error shown in the Figure 3.43?



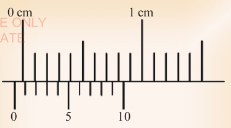
(a) 0.3 mm.
(b) 0.7 mm.
(c) -0.3 mm.
(d) -0.7 mm.

Section B
6. (a) From the list given below classify them in terms of regular or irregular shape.
cube, orange, stone, banana, water pipe, a house, cuboid, chalkboard.
(b) The internal and external radius of a hollow silver sphere are 7 cm and 14 cm, respectively. Find its volume.

7. (a) Write down the principal steps used in reading the vernier caliper.
(b) In a vernier calliper, there are 10 divisions on the vernier scale and 1 cm on main scale is divided in 10 parts. While measuring a length, the zero of the vernier scale lies just ahead of 1.8 cm mark and 4th division of vernier scale coincides with a main scale division. Find the value of the length.

8. (a) Differentiate between the mass and the volume of a substance.
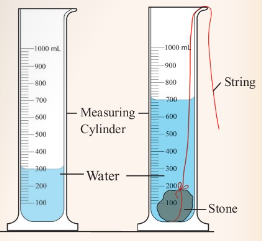
(b) Figure 3.44 shows a measuring cylinder containing water before and after a stone is immersed. What is the volume of the stone?



9. (a) Figure 3.45 shows a metre rule being used to measure the length of a textbook.



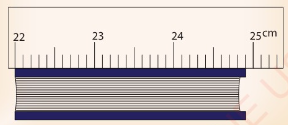
What is the approximate length of the book?
(b) Explain why it is advised to start at the mark beyond 1 cm when taking a measurement using a metre rule.

10. A physics student obtained the following results for the diameter of the same wire from an experiment: 0.35 mm, 0.36 mm and 0.34 mm. Calculate the diameter of the wire.

11. A rectangular block measures height 1.00 cm, width 2.50 cm, and length 4.00 cm.
(a) What instrument was used to measure the sides of the rectangular block?
(b) Calculate the volume of the rectangular block.